题目内容
5.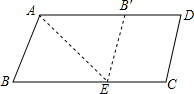 如图,将?ABCD对折,使AB与AD边重合,并且点B落在AD上的点B′处,折痕为AE,再将图形展开,得到四边形ABEB′,请你判断四边形ABEB′是否为菱形,并说明理由.
如图,将?ABCD对折,使AB与AD边重合,并且点B落在AD上的点B′处,折痕为AE,再将图形展开,得到四边形ABEB′,请你判断四边形ABEB′是否为菱形,并说明理由.
分析 由平行四边形的性质得到AD∥BC,∠B+∠BAD=180°,由对折有AB=AB′,∠B=∠AB′E,即可.
解答 解:四边形ABEB′是菱形.
理由如下:
由对折有AB=AB′,∠B=∠B′,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠B+∠BAD=180°
∵∠B=∠B′,
∴∠B′+∠BAD=180°,
∴AB∥B′E,
∵AD∥BC,
∴四边形ABEB′是平行四边形,
∵AB=AB′,
∴平行四边形ABEB′是菱形.
点评 此题是对折问题,主要考查了对折的性质,平行四边形的性质和判定,判断四边形ABEB′是平行四边形是解本题的关键.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
10.某灯泡厂生产节能灯泡1000只,其中有5只是次品,如果从中任取1只,这只灯泡是次品的概率是( )
| A. | $\frac{1}{1000}$ | B. | $\frac{1}{500}$ | C. | $\frac{1}{200}$ | D. | $\frac{95}{1000}$ |
17.八(6)班组织了一次经典朗读比赛,甲、乙两队各9人的比赛成绩如表(10分制):
(1)甲队成绩的中位数是10分,乙队成绩的众数是9分;
(2)计算乙队的平均成绩和方差;
(3)若选择其中一队参加校级经典朗读比赛则应选乙队.
| 甲 | 7 | 8 | 9 | 7 | 10 | 10 | 10 | 10 | 10 |
| 乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 |
(2)计算乙队的平均成绩和方差;
(3)若选择其中一队参加校级经典朗读比赛则应选乙队.

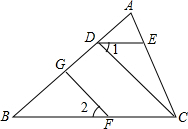 如图,已知DE∥BC,∠1=∠2,FG⊥AB,垂足为G,试说明CD⊥AB.
如图,已知DE∥BC,∠1=∠2,FG⊥AB,垂足为G,试说明CD⊥AB.