题目内容
5.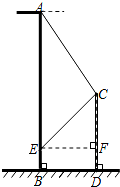 如图,已知楼AB高36米,从楼顶A处测得旗杆顶C的俯角为60°,又从该楼离地面6米的一窗口E处测得旗杆顶C的仰角为45°,求该旗杆CD的高.(结果保留根号)
如图,已知楼AB高36米,从楼顶A处测得旗杆顶C的俯角为60°,又从该楼离地面6米的一窗口E处测得旗杆顶C的仰角为45°,求该旗杆CD的高.(结果保留根号)
分析 过点C作CG⊥AE,垂足为点G,由题意得∠CEF=45°=∠CEG,∠ACG=60°,设CG=x,在Rt△ACG中,AG=CG•tan∠ACG=$\sqrt{3}$x,在Rt△ECG中,EG=CG•cot∠CEG=x,根据AG+EG=AE,列方程$\sqrt{3}x+x$=36-6,得到CF=EG=15$\sqrt{3}$-15,于是得到结论.
解答  解:过点C作CG⊥AE,垂足为点G,
解:过点C作CG⊥AE,垂足为点G,
由题意得∠CEF=45°=∠CEG,∠ACG=60°,
设CG=x,
在Rt△ACG中,AG=CG•tan∠ACG=$\sqrt{3}$x,
在Rt△ECG中,EG=CG•cot∠CEG=x,
∵AG+EG=AE,
∴$\sqrt{3}x+x$=36-6,
解得:x=15$\sqrt{3}$-15,
∴CF=EG=15$\sqrt{3}$-15,
∴CD=15$\sqrt{3}$-15+6=15$\sqrt{3}$-9.
答:该旗杆CD的高为(15$\sqrt{3}$-9)米.
点评 此题主要考查了仰角与俯角问题,正确应用锐角三角函数关系是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.若将抛物线平移,得到新抛物线y=(x+3)2,则下列平移方法中,正确的是( )
| A. | 向左平移3个单位 | B. | 向右平移3个单位 | C. | 向上平移3个单位 | D. | 向下平移3个单位 |
10.两个相似三角形的相似比是2:3,则这两个三角形的面积比是( )
| A. | $\sqrt{2}$:$\sqrt{3}$ | B. | 2:3 | C. | 2:5 | D. | 4:9 |
14.若两个相似三角形的周长之比是1:2,则它们的面积之比是( )
| A. | 1:2 | B. | 1:$\sqrt{2}$ | C. | 2:1 | D. | 1:4 |
 如图,在△ABC中,∠ACB=90°,若点G是△ABC的重心,cos∠BCG=$\frac{2}{3}$,BC=4,则CG=2.
如图,在△ABC中,∠ACB=90°,若点G是△ABC的重心,cos∠BCG=$\frac{2}{3}$,BC=4,则CG=2.