题目内容
20. 如图,在△ABC中,∠ACB=90°,若点G是△ABC的重心,cos∠BCG=$\frac{2}{3}$,BC=4,则CG=2.
如图,在△ABC中,∠ACB=90°,若点G是△ABC的重心,cos∠BCG=$\frac{2}{3}$,BC=4,则CG=2.
分析 延长CG交AB于D,作DE⊥BC于E,根据重心的概念得到点D为AB的中点,根据直角三角形的性质得到DC=DB,根据等腰三角形的三线合一得到CE=2,根据余弦的概念求出CD,根据三角形的重心的概念得到答案.
解答 解: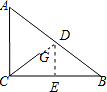 延长CG交AB于D,作DE⊥BC于E,
延长CG交AB于D,作DE⊥BC于E,
∵点G是△ABC的重心,
∴点D为AB的中点,
∴DC=DB,又DE⊥BC,
∴CE=BE=$\frac{1}{2}$BC=2,又cos∠BCG=$\frac{2}{3}$,
∴CD=3,
∵点G是△ABC的重心,
∴CG=$\frac{2}{3}$CD=2,
故答案为:2.
点评 本题考查的是三角形的重心的概念和性质以及锐角三角函数的定义,掌握三角形的重心是三角形三条中线的交点,且重心到顶点的距离是它到对边中点的距离的2倍是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.⊙O的半径为1,同一平面内,若点P与圆心O的距离为1,则点P与⊙O的位置关系是( )
| A. | 点P在⊙O外 | B. | 点P在⊙O上 | C. | 点P在⊙O内 | D. | 无法确定 |
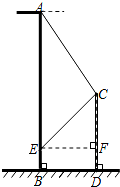 如图,已知楼AB高36米,从楼顶A处测得旗杆顶C的俯角为60°,又从该楼离地面6米的一窗口E处测得旗杆顶C的仰角为45°,求该旗杆CD的高.(结果保留根号)
如图,已知楼AB高36米,从楼顶A处测得旗杆顶C的俯角为60°,又从该楼离地面6米的一窗口E处测得旗杆顶C的仰角为45°,求该旗杆CD的高.(结果保留根号) 如图,在△ABC中,∠C=90°,AD平分∠CAB,AC=3,AD=4,则点D到直线AB的距离是$\sqrt{7}$.
如图,在△ABC中,∠C=90°,AD平分∠CAB,AC=3,AD=4,则点D到直线AB的距离是$\sqrt{7}$.