题目内容
若点P(2-a,a-3)在第四象限,则a的取值范围为( )
| A、a<2 | B、a<3 |
| C、2<a<3 | D、以上都不对 |
考点:点的坐标,解一元一次不等式组
专题:
分析:根据第四象限内点的横坐标是正数,纵坐标是负数列出不等式,然后求解即可.
解答:
解:∵点P(2-a,a-3)在第四象限,
∴
,
解不等式①得,a<2,
解不等式②得,a<3,
所以,a的取值范围是a<2.
故选A.
∴
|
解不等式①得,a<2,
解不等式②得,a<3,
所以,a的取值范围是a<2.
故选A.
点评:本题考查了各象限内点的坐标的符号特征以及解不等式,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).

练习册系列答案
相关题目
将方程x2-6x+5=0化成(x+m)2=n的形式,则m,n分别是( )
| A、m=-3,n=4 |
| B、m=3,n=-4 |
| C、m=-1,n=-5 |
| D、m=-5,n=-1 |
如图,这几个车标,是中心对称图形而不是轴对称图形的共有( )


| A、0个 | B、1个 | C、2个 | D、3个 |
 若有理数在数轴上的位置如图所示,则下列各式中一定成立的是( )
若有理数在数轴上的位置如图所示,则下列各式中一定成立的是( )| A、-a<0 | B、a+b<0 |
| C、a-b>0 | D、-ab>0 |
下列各式能用平方差公式分解因式的个数是( )
(1)x2+y2;(2)-x2+y2;(3)x2-y2;(4)-x2-y2.
(1)x2+y2;(2)-x2+y2;(3)x2-y2;(4)-x2-y2.
| A、1个 | B、2个 | C、3个 | D、4个 |
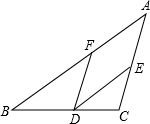 请将下面证明中的每一步的理由填在相应的括号内:
请将下面证明中的每一步的理由填在相应的括号内: