题目内容
9. 己知:如图,在梯形ABCD中,点E、F分别在AB、CD上,AD∥EF∥BC,CE平分∠BCD,AE:EB=1:2,AD=4,BC=10,求CD的长.
己知:如图,在梯形ABCD中,点E、F分别在AB、CD上,AD∥EF∥BC,CE平分∠BCD,AE:EB=1:2,AD=4,BC=10,求CD的长.
分析 连接AC交EF于M,由平行线分线段成比例定理得出$\frac{EM}{BC}=\frac{AE}{AB}$=$\frac{1}{3}$,$\frac{MF}{AD}=\frac{CF}{CD}$=$\frac{2}{3}$,$\frac{DF}{CF}$=$\frac{AE}{EB}$=$\frac{1}{2}$,求出EM=$\frac{10}{3}$,MF=$\frac{8}{3}$,得出EF=EM+MF=6,由平行线的性质和角平分线得出∠FEC=∠FCE,证出CF=EF=6,得出CD=$\frac{3}{2}$CF=9即可.
解答 解:连接AC交EF于M,如图所示: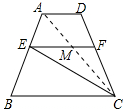
∵AE:EB=1:2,AD∥EF∥BC,
∴$\frac{EM}{BC}=\frac{AE}{AB}$=$\frac{1}{3}$,$\frac{MF}{AD}=\frac{CF}{CD}$=$\frac{2}{3}$,$\frac{DF}{CF}$=$\frac{AE}{EB}$=$\frac{1}{2}$,
即$\frac{EM}{10}=\frac{1}{3}$,$\frac{MF}{4}$=$\frac{2}{3}$,
解得:EM=$\frac{10}{3}$,MF=$\frac{8}{3}$,
∴EF=EM+MF=6,
∵EF∥BC,CE平分∠BCD,
∴∠FEC=∠BCE,∠FCE=∠BCE,
∴∠FEC=∠FCE,
∴CF=EF=6,
∴CD=$\frac{3}{2}$CF=$\frac{3}{2}$×6=9.
点评 本题考查了平行线分线段成比例定理、比例的性质、等腰三角形的判定;熟练掌握平行线分线段成比例定理,证出CF=EF是解决问题的关键.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
 如图,∠A=∠B=90°,M是AB的中点,DM平分∠ADC,求证:AD+BC=CD.
如图,∠A=∠B=90°,M是AB的中点,DM平分∠ADC,求证:AD+BC=CD. 有理数a,-b在数轴上的位置如图所示,化简:|1-3b|-2|2+b|+|2-3a|.
有理数a,-b在数轴上的位置如图所示,化简:|1-3b|-2|2+b|+|2-3a|. 如图,已知△ABC和△DAE,D是AC上一点,AD=AB,DE∥AB,DE=AC.求证:AE=BC.
如图,已知△ABC和△DAE,D是AC上一点,AD=AB,DE∥AB,DE=AC.求证:AE=BC. 如图,已知AB=AE,BC=ED,CF=FD,AC=AD.求证:∠BAF=∠EAF.
如图,已知AB=AE,BC=ED,CF=FD,AC=AD.求证:∠BAF=∠EAF. 如图,将△ABC的∠A沿DE折叠,探索∠1,∠2,∠A之间的数量关系2∠A=∠1-∠2.
如图,将△ABC的∠A沿DE折叠,探索∠1,∠2,∠A之间的数量关系2∠A=∠1-∠2.