题目内容
6.在平面直角坐标系中,点O为原点,平行于x轴的直线与抛物线L:y=ax2相交于A,B两点(点B在第一象限),点D在AB的延长线上.(1)已知a=1,点B的纵坐标为2.
①如图1,向右平移抛物线L使该抛物线过点B,与AB的延长线交于点C,求AC的长.
②如图2,若BD=$\frac{1}{2}$AB,过点B,D的抛物线L2,其顶点M在x轴上,求该抛物线的函数表达式.
(2)如图3,若BD=AB,过O,B,D三点的抛物线L3,顶点为P,对应函数的二次项系数为a3,过点P作PE∥x轴,交抛物线L于E,F两点,求$\frac{{a}_{3}}{a}$的值,并直接写出$\frac{AB}{EF}$的值.

分析 (1)①根据函数解析式求出点A、B的坐标,求出AC的长;
②作抛物线L2的对称轴与AD相交于点N,根据抛物线的轴对称性求出OM,利用待定系数法求出抛物线的函数表达式;
(2)过点B作BK⊥x轴于点K,设OK=t,得到OG=4t,利用待定系数法求出抛物线的函数表达式,根据抛物线过点B(t,at2),求出$\frac{{a}_{3}}{a}$的值,根据抛物线上点的坐标特征求出$\frac{AB}{EF}$的值.
解答 解:(1)①二次函数y=x2,当y=2时,2=x2,
解得x1=$\sqrt{2}$,x2=-$\sqrt{2}$,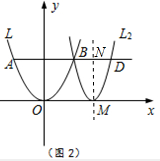
∴AB=2$\sqrt{2}$.
∵平移得到的抛物线L1经过点B,
∴BC=AB=2$\sqrt{2}$,
∴AC=4$\sqrt{2}$.
②作抛物线L2的对称轴与AD相交于点N,如图2,
根据抛物线的轴对称性,得BN=$\frac{1}{2}$DB=$\frac{\sqrt{2}}{2}$,
∴OM=$\frac{3\sqrt{2}}{2}$.
设抛物线L2的函数表达式为y=a(x-$\frac{3\sqrt{2}}{2}$)2,
由①得,B点的坐标为($\sqrt{2}$,2),
∴2=a($\sqrt{2}$-$\frac{3\sqrt{2}}{2}$)2,
解得a=4.
抛物线L2的函数表达式为y=4(x-$\frac{3\sqrt{2}}{2}$)2;
(2)如图3,抛物线L3与x轴交于点G,其对称轴与x轴交于点Q,
过点B作BK⊥x轴于点K,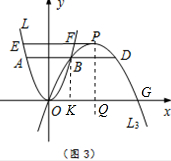
设OK=t,则AB=BD=2t,点B的坐标为(t,at2),
根据抛物线的轴对称性,得OQ=2t,OG=2OQ=4t.
设抛物线L3的函数表达式为y=a3x(x-4t),
∵该抛物线过点B(t,at2),
∴at2=a3t(t-4t),
∵t≠0,
∴$\frac{{a}_{3}}{a}$=-$\frac{1}{3}$,
由题意得,点P的坐标为(2t,-4a3t2),
则-4a3t2=ax2,
解得,x1=-$\frac{2\sqrt{3}}{3}$t,x2=$\frac{2\sqrt{3}}{3}$t,
EF=$\frac{4\sqrt{3}}{3}$t,
∴$\frac{AB}{EF}$=$\frac{\sqrt{3}}{2}$.
点评 本题考查的是二次函数的图象和性质、待定系数法求函数解析式,灵活运用待定系数法求出函数解析式、掌握抛物线的对称性、正确理解抛物线上点的坐标特征是解题的关键.

| A. | 为了了解全市中学生课外阅读情况,选择全面调查 | |
| B. | 为了了解全国中学生“母亲节”孝敬母亲的情况,选择全面调查 | |
| C. | 为了了解一批手机的使用寿命,选择抽样调查 | |
| D. | 旅客上飞机前的安检,选择抽样调查 |
| A. | a•a=a2 | B. | 2a+a=3a | C. | (a3)2=a5 | D. | a3÷a-1=a4 |
| A. | x2+2x=3x2 | B. | x6÷x2=x3 | C. | x2•(2x3)=2x5 | D. | (3x2)2=6x2 |
 如图,正六边形ABCDEF中,P、Q两点分别为△ACF、△CEF的内心.若AF=2,则PQ的长度为何?( )
如图,正六边形ABCDEF中,P、Q两点分别为△ACF、△CEF的内心.若AF=2,则PQ的长度为何?( )| A. | 1 | B. | 2 | C. | 2$\sqrt{3}$-2 | D. | 4-2$\sqrt{3}$ |
 如图,直角△ABC内接于⊙O,点D是直角△ABC斜边AB上的一点,过点D作AB的垂线交AC于E,过点C作∠ECP=∠AED,CP交DE的延长线于点P,连结PO交⊙O于点F.
如图,直角△ABC内接于⊙O,点D是直角△ABC斜边AB上的一点,过点D作AB的垂线交AC于E,过点C作∠ECP=∠AED,CP交DE的延长线于点P,连结PO交⊙O于点F. 如图,D、E是△ABC边AB、AC上的两点,AD:DB=2:1,DE∥BC,记$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,那么$\overrightarrow{DE}$=$\frac{2}{3}$$\overrightarrow{b}$-$\frac{2}{3}$$\overrightarrow{a}$(用$\overrightarrow{a}$,$\overrightarrow{b}$表示).
如图,D、E是△ABC边AB、AC上的两点,AD:DB=2:1,DE∥BC,记$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,那么$\overrightarrow{DE}$=$\frac{2}{3}$$\overrightarrow{b}$-$\frac{2}{3}$$\overrightarrow{a}$(用$\overrightarrow{a}$,$\overrightarrow{b}$表示). 如图,在一次数学课外实践活动中,小聪在距离旗杆10m的A处测得旗杆顶端B的仰角为60°,测角仪高AD为1m,则旗杆高BC为10$\sqrt{3}$+1m(结果保留根号).
如图,在一次数学课外实践活动中,小聪在距离旗杆10m的A处测得旗杆顶端B的仰角为60°,测角仪高AD为1m,则旗杆高BC为10$\sqrt{3}$+1m(结果保留根号). )﹣3+
)﹣3+ ﹣(
﹣( )0
)0