��Ŀ����
��֪������y=ax2+bx+c��x�ύ��A����2��0����B��4��0�����㣬����C��x��ľ���Ϊ2����������ߵĽ���ʽΪ______��
y=��x2+x+��y=x2��x�� ����������������������������ߵĶԳ��Ե������ߵĶԳ���Ϊֱ��x=1�����ȷ��C������Ϊ��1��2����1��-2�����������߽���ʽΪy=a��x+2����x-4����Ȼ���C��1��2����1��-2���ֱ���������Ӧ��a��ֵ���Ӷ��õ���Ӧ�����ߵĽ���ʽ�� �⣺��������y=ax2+bx+c��x�ύ��A����2��0����B��4��0�����㣬 �������ߵĶԳ���Ϊֱ��x=...
��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
�����±��еĶ��κ���y=ax2+bx+c���Ա���x�뺯��y�Ķ�Ӧֵ�����ж϶��κ����Ľ���ʽΪ��������
x | �� |
| 0 | 1 | 2 | �� |
y | �� |
|
|
|
| �� |
A. y=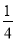 x2��
x2��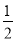 x��
x��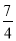 B. y=
B. y=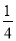 x2+
x2+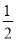 x��
x��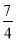
C. y=��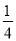 x2��
x2��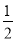 x+
x+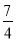 D. y=��
D. y=��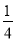 x2+
x2+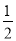 x+
x+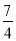


 B.
B.  C.
C.  D.
D. 
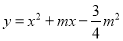 ��m��0����x�ύ��A��B���㣮
��m��0����x�ύ��A��B���㣮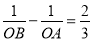 ��OΪ����ԭ�㣩���������ߵĽ���ʽ��
��OΪ����ԭ�㣩���������ߵĽ���ʽ��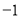
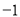
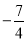
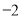
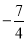
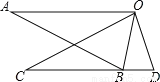
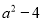 ��ʽ�ֽ�Ľ����_____________________��
��ʽ�ֽ�Ľ����_____________________��