题目内容
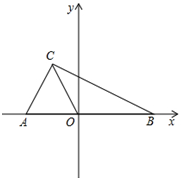 如图,在平面直角坐标系中,A(a,0),B(b,0),C(-1,2),且|2a+b+1|+(a+2b-4)2=0.
如图,在平面直角坐标系中,A(a,0),B(b,0),C(-1,2),且|2a+b+1|+(a+2b-4)2=0.(1)求a,b的值;
(2)①在x轴的正半轴上存在一点M,使S△COM=
| 1 |
| 2 |
②在坐标轴的其它位置是否存在点M,使S△COM=
| 1 |
| 2 |
考点:坐标与图形性质,三角形的面积
专题:
分析:(1)根据非负数的性质列出关于a、b的二元一次方程组,求解即可;
(2)①根据三角形的面积公式列式求出OM的长,然后写出点M的坐标即可;
②写出点M在x轴负半轴上时的坐标,再求出点M在y轴上,根据三角形的面积公式列式求出OM的长,然后写出点M的坐标.
(2)①根据三角形的面积公式列式求出OM的长,然后写出点M的坐标即可;
②写出点M在x轴负半轴上时的坐标,再求出点M在y轴上,根据三角形的面积公式列式求出OM的长,然后写出点M的坐标.
解答:解:(1)由题意得,
,
①×2得,4a+2b+2=0③,
③-②得,3a=-6,
解得a=-2,
把a=-2代入①得,-4+b+1=0,
解得b=3;
(2)∵a=-2,b=3,C(-1,2),
∴AB=3-(-2)=5,点C到AB的距离为2,
∴
OM•2=
×
×5×2,
解得OM=2.5,
∵点M在x轴正半轴上,
∴M的坐标为(2.5,0);
②存在.
点M在x轴负半轴上时,点M(-2.5,0),
点M在y轴上时,
OM•1=
×
×5×2,
解得OM=5,
所以,点M的坐标为(0,5)或(0,-5),
综上所述,存在点M的坐标为(0,5)或(-2.5,0)或(0,-5).
|
①×2得,4a+2b+2=0③,
③-②得,3a=-6,
解得a=-2,
把a=-2代入①得,-4+b+1=0,
解得b=3;
(2)∵a=-2,b=3,C(-1,2),
∴AB=3-(-2)=5,点C到AB的距离为2,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得OM=2.5,
∵点M在x轴正半轴上,
∴M的坐标为(2.5,0);
②存在.
点M在x轴负半轴上时,点M(-2.5,0),
点M在y轴上时,
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得OM=5,
所以,点M的坐标为(0,5)或(0,-5),
综上所述,存在点M的坐标为(0,5)或(-2.5,0)或(0,-5).
点评:本题考查了坐标与图形性质,三角形的面积,非负数的性质,二元一次方程组的解法,(1)几个非负数的和为0时,这几个非负数都为0;(2)要注意题目条件对点M的要求.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若a=-0.22,b=-2-2,c=(-
)-2,d=(-
)0,则( )
| 1 |
| 2 |
| 1 |
| 5 |
| A、a<b<c<d |
| B、b<a<d<c |
| C、a<b<d<c |
| D、c<a<d<b |
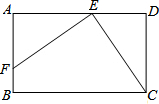 如图,在矩形ABCD中,E为AD上的一点,EF⊥CE交AB于F,且CE=EF,
如图,在矩形ABCD中,E为AD上的一点,EF⊥CE交AB于F,且CE=EF, 如图,已知∠1+∠2=180°,∠B=∠3,求证:DE∥BC.
如图,已知∠1+∠2=180°,∠B=∠3,求证:DE∥BC.