题目内容
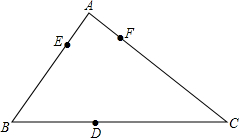 如图,D、E、F分别是△ABC中边BC、AB、AC上的点,且AE=AF,BE=BD,CF=CD,已知AB=4,AC=3,BD•DC=6,求△ABC的面积.
如图,D、E、F分别是△ABC中边BC、AB、AC上的点,且AE=AF,BE=BD,CF=CD,已知AB=4,AC=3,BD•DC=6,求△ABC的面积.考点:勾股定理的逆定理
专题:
分析:设BE=x,CF=y,则AE=4-x,AF=3-y,BE=BD=x,CF=CD=y,因为BD•DC=6,AE=AF,所以
,解得:
,然后由勾股定理的逆定理,可以判断△ABC是Rt△,然后由三角形的面积公式计算即可.
|
|
解答:解:设BE=x,CF=y,则AE=4-x,AF=3-y,BE=BD=x,CF=CD=y,
∵BD•DC=6,AE=AF,
∴
,
解得:
,
∴BC=5,
∵AB2+AC2=32+42=25=52=BC2,
∴△ABC是Rt△,
∵S△ABC=
•AB•AC
∴S△ABC=
×3×4=6.
∵BD•DC=6,AE=AF,
∴
|
解得:
|
∴BC=5,
∵AB2+AC2=32+42=25=52=BC2,
∴△ABC是Rt△,
∵S△ABC=
| 1 |
| 2 |
∴S△ABC=
| 1 |
| 2 |
点评:此题考查了勾股定理的逆定理,解题的关键是求出BC的值,然后判断△ABC为Rt△.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
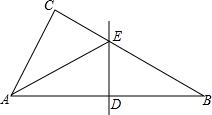 如图,在△ABC中,∠C=90°,E为BC边上一点,将△CAE沿AE折叠,C的对应点D恰好落在AB的中点上,求∠B的度数.
如图,在△ABC中,∠C=90°,E为BC边上一点,将△CAE沿AE折叠,C的对应点D恰好落在AB的中点上,求∠B的度数.