题目内容
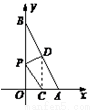
一次函数y=kx+b的图象与x、y轴分别交于点A(2,0),B(0,4).
(1)求该函数的解析式;
(2)O为坐标原点,设OA、AB的中点分别为C、D,P为OB上一动点,求PC+PD的最小值,并求取得最小值时P点的坐标.
练习册系列答案
相关题目
12.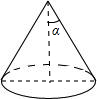 如图,圆锥的底面半径为3,侧面积为18π,设圆锥的母线与高的夹角为α,则tanα的值是( )
如图,圆锥的底面半径为3,侧面积为18π,设圆锥的母线与高的夹角为α,则tanα的值是( )
 如图,圆锥的底面半径为3,侧面积为18π,设圆锥的母线与高的夹角为α,则tanα的值是( )
如图,圆锥的底面半径为3,侧面积为18π,设圆锥的母线与高的夹角为α,则tanα的值是( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | 2 |


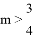 B.
B. 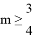 C.
C.  的倒数是( )
的倒数是( ) B.
B.  C.
C. 
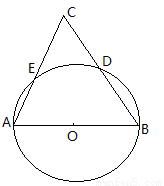
 的两根分别为
的两根分别为 ,
,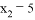 ,那么这个一元二次方程是______.
,那么这个一元二次方程是______. 如图,在平面直角坐标系xOy中,二次函数y=x2-3x的图象与x轴相交于O、A两点.
如图,在平面直角坐标系xOy中,二次函数y=x2-3x的图象与x轴相交于O、A两点.