题目内容
11.已知关于x的一元二次方程ax2+bx+c=0的一个根为x=1,且a,b满足等式b=$\frac{\sqrt{{a}^{2}-16}+\sqrt{16-{a}^{2}}-2}{a+4}$.试求方程$\frac{1}{4}$y2+c=0的根.分析 根据一元二次方程ax2+bx+c=0的一个根为x=1,得a+b+c=0,再由a,b满足等式b=$\frac{\sqrt{{a}^{2}-16}+\sqrt{16-{a}^{2}}-2}{a+4}$,得a=4,b=-$\frac{1}{4}$,得出c代入方程$\frac{1}{4}$y2+c=0,求得根即可.
解答 解:∵一元二次方程ax2+bx+c=0的一个根为x=1,
∴a+b+c=0,
∵a,b满足等式b=$\frac{\sqrt{{a}^{2}-16}+\sqrt{16-{a}^{2}}-2}{a+4}$,
∴a=4,b=-$\frac{1}{4}$,
∴c=-$\frac{15}{4}$,
∴方程$\frac{1}{4}$y2-$\frac{15}{4}$=0,
∴y=$±\sqrt{15}$,
y1=$\sqrt{15}$,y2=-$\sqrt{15}$.
点评 本题考查了一元二次方程的解,以及二次根式有意义的条件,若a2-16=0,a=±4,注意分母不为0.

练习册系列答案
相关题目
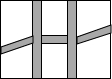 某单位院内有一块长30m,宽20m的矩形空地,准备将其建成一个矩形花坛,要求在花坛中修两条纵向平行和横向弯折的小道(如图),剩余的地方种植花草,要使种植花草的面积为532m2,那么小道进出口的宽度应为多少米?(注:左右小道进出口的宽度相等,且每段小道均为平行四边形)
某单位院内有一块长30m,宽20m的矩形空地,准备将其建成一个矩形花坛,要求在花坛中修两条纵向平行和横向弯折的小道(如图),剩余的地方种植花草,要使种植花草的面积为532m2,那么小道进出口的宽度应为多少米?(注:左右小道进出口的宽度相等,且每段小道均为平行四边形)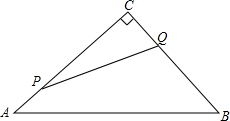 如图,在Rt△ABC中,∠C=90°,AC=30cm,BC=21cm,动点P从点C出发,沿CA方向运动,动点Q从点B出发,沿BC方向运动,如果点P,Q的运动速度均为1cm/s.那么运动几秒时,它们相距15cm?
如图,在Rt△ABC中,∠C=90°,AC=30cm,BC=21cm,动点P从点C出发,沿CA方向运动,动点Q从点B出发,沿BC方向运动,如果点P,Q的运动速度均为1cm/s.那么运动几秒时,它们相距15cm?