题目内容
19.已知y=$\sqrt{\frac{{x}^{2}-2}{5x-4}}$-$\sqrt{\frac{{x}^{2}-2}{4-5x}}$+2,则x2+y2=6.分析 先根据二次根式及分式有意义的条件求出x,y的值,进而可得出结论.
解答 解:∵$\sqrt{\frac{{x}^{2}-2}{5x-4}}$与$\sqrt{\frac{{x}^{2}-2}{4-5x}}$有意义,
∴$\left\{\begin{array}{l}\frac{{x}^{2}-2}{5x-4}≥0\\ \frac{{x}^{2}-2}{5x-4}≥0\end{array}\right.$,
∴$\left\{\begin{array}{l}{x}^{2}-2=0\\ 5x-4≠0\end{array}\right.$,解得x2=2且x≠$\frac{4}{5}$,
∴y2=4,
∴x2+y2=2+4=6.
故答案为:6.
点评 本题考查的是二次根式有意义的条件,熟知二次根式具有非负性是解答此题的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
7.如表给出了某班5名学生身高情况(单位:cm).
(1)完成表中空的部分;
(2)他们5人中最高身高比最矮身高高多少?
(3)如果身高到达或超过平均身高时叫达标身高,那么这5个同学身高的达标率是多少(精确0.01)?
| 学生 | A | B | C | D | E |
| 身高(单位:cm) | 165 | 168 | 166 | 163 | 173 |
| 身高与班级平均身高的差值 | -1 | +2 | 0 | -3 |
(2)他们5人中最高身高比最矮身高高多少?
(3)如果身高到达或超过平均身高时叫达标身高,那么这5个同学身高的达标率是多少(精确0.01)?
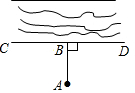 如图,要把池中的水引到CD处,可过A点引AB⊥CD于B,然后沿AB开渠,可使所开渠道最短,试说明设计的依据:垂线段最短.
如图,要把池中的水引到CD处,可过A点引AB⊥CD于B,然后沿AB开渠,可使所开渠道最短,试说明设计的依据:垂线段最短.