题目内容
18.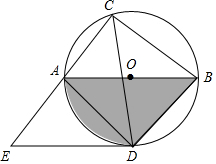 如图,⊙O的直径AB=10,弦AC=6,∠ACB的平分线交⊙O于D,过点D作DE∥AB交CA的延长线于点E,连接AD,BD.
如图,⊙O的直径AB=10,弦AC=6,∠ACB的平分线交⊙O于D,过点D作DE∥AB交CA的延长线于点E,连接AD,BD.(1)由AB,BD,$\widehat{AD}$围成的曲边三角形的面积是$\frac{25}{2}$+$\frac{25π}{4}$;
(2)求证:DE是⊙O的切线;
(3)求线段DE的长.
分析 (1)连接OD,由AB是直径知∠ACB=90°,结合CD平分∠ACB知∠ABD=∠ACD=$\frac{1}{2}$∠ACB=45°,从而知∠AOD=90°,根据曲边三角形的面积=S扇形AOD+S△BOD可得答案;
(2)由∠AOD=90°,即OD⊥AB,根据DE∥AB可得OD⊥DE,即可得证;
(3)勾股定理求得BC=8,作AF⊥DE知四边形AODF是正方形,即可得DF=5,由∠EAF=90°-∠CAB=∠ABC知tan∠EAF=tan∠CBA,即$\frac{EF}{AF}$=$\frac{AC}{BC}$,求得EF的长即可得.
解答 解:(1)如图,连接OD,
∵AB是直径,且AB=10,
∴∠ACB=90°,AO=BO=DO=5,
∵CD平分∠ACB,
∴∠ABD=∠ACD=$\frac{1}{2}$∠ACB=45°,
∴∠AOD=90°,
则曲边三角形的面积是S扇形AOD+S△BOD=$\frac{90•π•{5}^{2}}{360}$+$\frac{1}{2}$×5×5=$\frac{25}{2}$+$\frac{25π}{4}$,
故答案为:$\frac{25}{2}$+$\frac{25π}{4}$;
(2)由(1)知∠AOD=90°,即OD⊥AB,
∵DE∥AB,
∴OD⊥DE,
∴DE是⊙O的切线;
(3)∵AB=10、AC=6,
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=8,
过点A作AF⊥DE于点F,则四边形AODF是正方形,
∴AF=OD=FD=5,
∴∠EAF=90°-∠CAB=∠ABC,
∴tan∠EAF=tan∠CBA,
∴$\frac{EF}{AF}$=$\frac{AC}{BC}$,即$\frac{EF}{5}$=$\frac{6}{8}$,
∴$EF=\frac{15}{4}$,
∴DE=DF+EF=$\frac{15}{4}$+5=$\frac{35}{4}$.
点评 本题主要考查切线的判定、圆周角定理、正方形的判定与性质及正切函数的定义,熟练掌握圆周角定理、切线的判定及三角函数的定义是解题的关键.

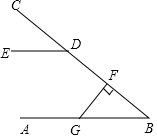 如图,AB∥DE,FG⊥BC于F,∠CDE=40°,则∠FGB=( )
如图,AB∥DE,FG⊥BC于F,∠CDE=40°,则∠FGB=( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
 如图是由若干小正方体组成的几何体的俯视图,小正方形中的数字表示该位置小正方体的个数,这个几何体的主视图是( )
如图是由若干小正方体组成的几何体的俯视图,小正方形中的数字表示该位置小正方体的个数,这个几何体的主视图是( )



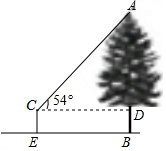 如图,创新小组要测量公园内一棵树的高度AB,其中一名小组成员站在距离树10米的点E处,测得树顶A的仰角为54°.已知测角仪的架高CE=1.5米,则这棵树的高度为15.3米.(结果保留一位小数.参考数据:sin54°=0.8090,cos54°=0.5878,tan54°=1.3764)
如图,创新小组要测量公园内一棵树的高度AB,其中一名小组成员站在距离树10米的点E处,测得树顶A的仰角为54°.已知测角仪的架高CE=1.5米,则这棵树的高度为15.3米.(结果保留一位小数.参考数据:sin54°=0.8090,cos54°=0.5878,tan54°=1.3764)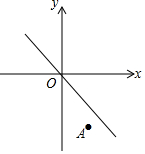 如图,将直线y=-x沿y轴向下平移后的直线恰好经过点A(2,-4),且与y轴交于点B,在x轴上存在一点P使得PA+PB的值最小,则点P的坐标为($\frac{2}{3}$,0).
如图,将直线y=-x沿y轴向下平移后的直线恰好经过点A(2,-4),且与y轴交于点B,在x轴上存在一点P使得PA+PB的值最小,则点P的坐标为($\frac{2}{3}$,0).