题目内容
3.已知x,y,z满足于|x-y|+$\sqrt{2y+z}$+z2-z+$\frac{1}{4}$=0,求x+y+z的立方根.分析 根据完全平方公式,可得非负数的和等于零,根据非负数的和为零,可得x,y、z的值,根据有理数的加法,可得x+y+z,根据开方运算,可得答案.
解答 解:原式等价于|x-y|+$\sqrt{2y+z}$+(z-$\frac{1}{2}$)2=0.
得
x-y=0,2y+z=0,z-$\frac{1}{2}$=0.
解得x=-$\frac{1}{4}$,y=-$\frac{1}{4}$,z=$\frac{1}{2}$,
x+y+z=0,0的立方根为0.
点评 本题考查了非负数的性质,利用非负数的性质得出x,y、z的值是解题关键.

练习册系列答案
相关题目
8.已知:x=-1,y=$\frac{1}{2}$,求x2-4xy+4y2的值,则正确的是( )
| A. | 2 | B. | -1 | C. | 0 | D. | 4 |
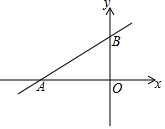 一次函数的图象与x轴、y轴分别交于点A(-4,0)和点B(0,3).
一次函数的图象与x轴、y轴分别交于点A(-4,0)和点B(0,3).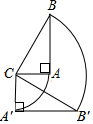 如图所示,将直角△ABC向下旋转90°,已知BC=5厘米,AB=4厘米,AC=3厘米,求△ABC扫过的面积.
如图所示,将直角△ABC向下旋转90°,已知BC=5厘米,AB=4厘米,AC=3厘米,求△ABC扫过的面积. 如图,点D,E分别为△ABC的边AB,BC的中点,若DE=3cm,则AC=6cm.
如图,点D,E分别为△ABC的边AB,BC的中点,若DE=3cm,则AC=6cm.