题目内容
15.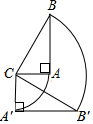 如图所示,将直角△ABC向下旋转90°,已知BC=5厘米,AB=4厘米,AC=3厘米,求△ABC扫过的面积.
如图所示,将直角△ABC向下旋转90°,已知BC=5厘米,AB=4厘米,AC=3厘米,求△ABC扫过的面积.
分析 根据旋转的性质得出直角△ABC扫过的面积是S扇形BAB′+S△ACB′进而求出即可.
解答 解:∵将此三角形绕点A顺时针旋转90°到直角△AB′C′的位置,
∴∠BAB′=90°,
∴直角△ABC扫过的面积是:S扇形BAB′+S△ACB′=$\frac{90π×{5}^{2}}{360}$+$\frac{1}{2}$×3×4=$\frac{25π}{4}$+6.
点评 此题主要考查了旋转的性质以及扇形面积求法,利用旋转性质得出旋转后图形的形状是解题关键.

练习册系列答案
相关题目
10.20142-2013×2015的计算结果是( )
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
11.Rt△ABC中,∠C为直角,AC=5,BC=12,那么下列∠A的四个三角函数中正确的是( )
| A. | sinA=$\frac{5}{13}$ | B. | cosA=$\frac{12}{13}$ | C. | tanA=$\frac{13}{12}$ | D. | $\frac{1}{tanA}$=$\frac{5}{12}$ |
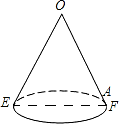 如图是一个底面直径为10,母线OE长也为10的圆锥,A是母线OF上的一点,FA=2,则圆锥的侧面积是50π,从点E沿圆锥侧面到点A的最短路径长是2$\sqrt{41}$.
如图是一个底面直径为10,母线OE长也为10的圆锥,A是母线OF上的一点,FA=2,则圆锥的侧面积是50π,从点E沿圆锥侧面到点A的最短路径长是2$\sqrt{41}$.