题目内容
13.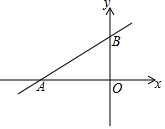 一次函数的图象与x轴、y轴分别交于点A(-4,0)和点B(0,3).
一次函数的图象与x轴、y轴分别交于点A(-4,0)和点B(0,3).(1)确定此一次函数的解析式;
(2)求坐标原点O到直线AB的距离;
(3)点P是线段AB上的一个动点,过点P作PD垂直于x轴于D,作PE垂直于y轴于E,记L=PD+PE,问L是否存在最大值和最小值?若存在,求出此时P点到原点O的距离,若不存在请说明理由.
分析 (1)设一次函数表达式为y=kx+b,经过A(-4,0)、B(0,3),代入解方程组即可.
(2)设坐标原点O到直线AB的距离为d,根据S△ABO=$\frac{1}{2}$×AO×BO=$\frac{1}{2}$×AB×d,即可解决问题.
(3)过点P作PD⊥x轴于D,作PE⊥y轴于E,设P(x,y),构建一次函数,根据自变量的取值范围以及一次函数的增减性即可解决问题.
解答 解:(1)设一次函数表达式为y=kx+b,经过A(-4,0)、B(0,3)
代入得$\left\{\begin{array}{l}{-4k+b=0}\\{b=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{3}{4}}\\{b=3}\end{array}\right.$.
∴一次函数解析式为y=$\frac{3}{4}$x+3.
(2)设坐标原点O到直线AB的距离为d,
在Rt△ABO中,OA=4,OB=3
根据勾股定理得AB=$\sqrt{{4}^{2}+{3}^{2}}$=5,
∵S△ABO=$\frac{1}{2}$×AO×BO=$\frac{1}{2}$×AB×d
即4×3=5d,
d=$\frac{12}{5}$,
∴原点O到直线AB的距离为$\frac{12}{5}$.
(3)过点P作PD⊥x轴于D,作PE⊥y轴于E,设P(x,y),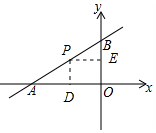
∵P点在线段AB上,
∴y=$\frac{3}{4}$x+3,其中-4≤x≤0,
∴L=PD+PE=-x+y=-x+$\frac{3}{4}$x+3=-$\frac{1}{4}$x+3,
∵-$\frac{1}{4}$<0,
∴L随x的增大而减小
∴当x=-4时,L最大=4,此时P点坐标为(-4,4),P点到原点O的距离为
PO=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$,
当x=0时,L最小=3,此时P点与B点重合,P点到原点O的距离为BO=3.
点评 本题考查一次函数综合题、待定系数法、一次函数的增减性、三角形的面积等知识,解题的关键是熟练运用所学知识解决问题,学会构建一次函数解决最值问题,属于中考常考题型.

①任何数都不等于它的相反数;
②一个数的绝对值一定是正数;
③表示互为相反数的两个数的点到原点的距离相等;
④若有理数a,b互为相反数,那么a+b=0;
⑤绝对值最小的数是0.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
(1)对照数轴填写表格:
| a | 6 | -6 | -6 | 2 | -1.5 |
| b | 4 | 0 | -4 | -10 | -1.5 |
| A、B两点的距离 | 2 | 0 |
(3)求出数轴上到7和-7的距离之和为14的所有整数的和;
(4)若点C表示的数为x,当点C在什么位置时,|x+1|+|x-2|取得的值最小.
(5)动点A从原点出发向数轴负方向运动,同时,动点B也从原点出发向数轴正方向运动.运动到3秒时,两点相距15个单位长度.已知动点A、B的速度之比是3:2(速度单位:1个单位长度/秒).求两个动点运动的速度.
| A. | 0 | B. | 2 | C. | -2 | D. | 4 |
