题目内容
14.已知一次函数的图象与y轴的交点为(0,-3),且与坐标轴围成的三角形的面积为6,求这个一次函数的表达式.分析 先把P点坐标代入y=kx+b可计算出b的值,再用k表示一次函数与x轴的交点坐标,然后根据三角形面积公式得到$\frac{1}{2}$×3×|$\frac{3}{k}$|=6,再解方程即可得到k的值.
解答 解:把P(0,-3)代入y=kx+b得b=-3,
把y=0代入y=kx-3得kx-3=0,
解得:x=$\frac{3}{k}$,则一次函数图象与x轴的交点坐标为($\frac{3}{k}$,0),
因为一次函数y=kx+b的图象与两坐标轴围成的三角形面积为6,
所以$\frac{1}{2}$×3×|$\frac{3}{k}$|=6,
解得:k=±$\frac{3}{4}$,
即这个一次函数的表达式为:y=±$\frac{3}{4}$x-3.
点评 本题考查了一次函数图形上点的坐标特征:一次函数y=kx+b,(k≠0,且k,b为常数)的图象是一条直线.它与x轴的交点坐标是(-$\frac{b}{k}$,0);与y轴的交点坐标是(0,b);直线上任意一点的坐标都满足函数关系式y=kx+b.

练习册系列答案
相关题目
4.下列结论正确的有( )
①任何数都不等于它的相反数;
②一个数的绝对值一定是正数;
③表示互为相反数的两个数的点到原点的距离相等;
④若有理数a,b互为相反数,那么a+b=0;
⑤绝对值最小的数是0.
①任何数都不等于它的相反数;
②一个数的绝对值一定是正数;
③表示互为相反数的两个数的点到原点的距离相等;
④若有理数a,b互为相反数,那么a+b=0;
⑤绝对值最小的数是0.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
2.已知x1、x2是一元二次方程x2-2x=0的两根,则x1•x2的值是( )
| A. | 0 | B. | 2 | C. | -2 | D. | 4 |
9.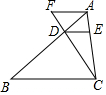 如图,已知点D、E分别在△ABC的边AB、AC上,DE∥BC,点F在CD延长线上,AF∥BC,则下列结论错误的是( )
如图,已知点D、E分别在△ABC的边AB、AC上,DE∥BC,点F在CD延长线上,AF∥BC,则下列结论错误的是( )
 如图,已知点D、E分别在△ABC的边AB、AC上,DE∥BC,点F在CD延长线上,AF∥BC,则下列结论错误的是( )
如图,已知点D、E分别在△ABC的边AB、AC上,DE∥BC,点F在CD延长线上,AF∥BC,则下列结论错误的是( )| A. | $\frac{DE}{AF}$=$\frac{AF}{BC}$ | B. | $\frac{FD}{AE}$=$\frac{DC}{EC}$ | C. | $\frac{AD}{AB}$=$\frac{AE}{AC}$ | D. | $\frac{BD}{AB}$=$\frac{DE}{AF}$ |
19.多项式-2(x-2)去括号得( )
| A. | -2x-2 | B. | -2x+2 | C. | -2x-4 | D. | -2x+4 |