题目内容
7.某校九年级(1)班准备购买大课间活动器材呼啦圈和跳绳,已知购买1根跳绳和2个呼啦圈要35元,购买2根跳绳和1个呼啦圈要25元.(1)求每根跳绳、每个呼啦圈各多少元?
(2)根据班级实际情况,需购买跳绳和呼啦圈的总数量为30,总费用不超过300元,但不低于280元,请你通过计算求出有几种购买方案,哪种方案费用最低.
分析 (1)根据题意可以列出相应的方程组,从而可以求得每根跳绳、每个呼啦圈各多少元;
(2)根据题意可以列出相应的不等式组,从而可以求得相应的购买方案和哪种购买方案费用最低.
解答 解:(1)每根跳绳x元,每个呼啦圈y元,
$\left\{\begin{array}{l}{x+2y=35}\\{2x+y=25}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=5}\\{y=15}\end{array}\right.$,
答:每根跳绳5元,每个呼啦圈15元;
(2)设需购买跳绳a根,
$\left\{\begin{array}{l}{5a+15(30-a)≤300}\\{5a+15(30-a)≥280}\end{array}\right.$,
解得,15≤a≤17,
∴有三种购买方案,
方案一:购买跳绳15根,购买呼啦圈15根,
方案二:购买跳绳16根,购买呼啦圈14根,
方案三:购买跳绳17根,购买呼啦圈13根,
∵跳绳比呼啦圈便宜,
∴方案三费用最低.
点评 本题考查二元一次方程组的应用、一元一次不等式组的应用,解答此类问题的关键是明确题意,找出所求问题需要的条件,利用方程的思想和不等式的思想解答.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目
12.农夫将苹果树种在正方形的果园内.为了保护苹果树不怕风吹,他在苹果树的周围种针叶树.在下图里,你可以看到农夫所种植苹果树的列数(n)和苹果树数量及针叶树数量的规律:当n为某一个数值时,苹果树数量会等于针叶树数量,则n为( )


| A. | 6 | B. | 8 | C. | 12 | D. | 16 |
16.若关于x的一元二次方程ax2-4x+1=0有两个相等实数根,则a的值是( )
| A. | -1 | B. | 1 | C. | -4 | D. | 4 |


 如图,AB与CD相交于点E,AC∥DB,△ACE与△BDE是位似图形吗?
如图,AB与CD相交于点E,AC∥DB,△ACE与△BDE是位似图形吗?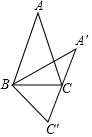 如图,在△ABC中,AB=AC,将△ABC绕顶点B顺时针旋转,得到△A′BC′.设∠A=α,当A′C′恰好经过顶点C时,∠A′BC=90°-$\frac{3α}{2}$(用含α的式子表示).
如图,在△ABC中,AB=AC,将△ABC绕顶点B顺时针旋转,得到△A′BC′.设∠A=α,当A′C′恰好经过顶点C时,∠A′BC=90°-$\frac{3α}{2}$(用含α的式子表示).