题目内容
4.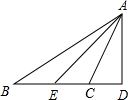 如图,在△ABC中,∠B=25°,∠ACB=105°,AD⊥BC,交BC的延长线于点D,AE平分∠BAC,求∠DAE的度数.
如图,在△ABC中,∠B=25°,∠ACB=105°,AD⊥BC,交BC的延长线于点D,AE平分∠BAC,求∠DAE的度数.
分析 先根据三角形内角和定理得出∠BAC的度数,再由角平分线的性质得出∠BAE的度数,由三角形外角的性质求出∠AEC的度数,进而可得出结论.
解答 解:∵在△ABC中,∠B=25°,∠ACB=105°,
∴∠BAC=180°-25°-105°=50°.
∵AE平分∠BAC,
∴∠BAE=$\frac{1}{2}$∠BAC=25°,
∴∠AEC=∠B+∠BAC=25°+25°=50°.
∵AD⊥BC,
∴∠D=90°,
∴∠DAE=90°-∠AED=90°-50°=40°.
点评 本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.已知正六边形的边长为2,则它的边心距为( )
| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
15.下列图形中,能用∠ABC,∠B,∠1表示同一个角的是( )
| A. |  | B. |  | C. |  | D. |  |
12.已知二次函数y=ax2+bx+c的x、y的部分对应值如下表:
则该函数的对称轴为( )
| X | … | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 5 | 1 | -1 | -1 | 1 | … |
| A. | y轴 | B. | 直线x=$\frac{3}{2}$ | C. | 直线x=2 | D. | 直线x=$\frac{5}{2}$ |
 如图,D为线段AC的中点,BC=$\frac{1}{4}$AB,BD=9,则线段AC的长为30.
如图,D为线段AC的中点,BC=$\frac{1}{4}$AB,BD=9,则线段AC的长为30.