题目内容
14.已知正六边形的边长为2,则它的边心距为( )| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
分析 连接OA、OB,作OC⊥AB于C,由正六边形的性质得出AC=BC=$\frac{1}{2}$AB=1,∠AOB=60°,得出∠AOC=30°,求出OC即可.
解答 解:如图所示: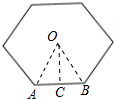
连接OA、OB,作OC⊥AB于C,
则∠OCA=90°,AC=BC=$\frac{1}{2}$AB=1,∠AOB=60°,
∴∠AOC=30°,
∴OC=$\sqrt{3}$AC=$\sqrt{3}$;
故选C.
点评 本题考查了正多边形和圆、正六边形的性质、三角函数等知识;熟练掌握正六边形的性质,求出AC是解决问题的关键.

练习册系列答案
相关题目
5.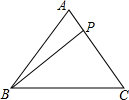 如图,在△ACB中,有一点P在AC上移动,若AB=AC=5,BC=6,则AP+BP+CP的最小值为( )
如图,在△ACB中,有一点P在AC上移动,若AB=AC=5,BC=6,则AP+BP+CP的最小值为( )
 如图,在△ACB中,有一点P在AC上移动,若AB=AC=5,BC=6,则AP+BP+CP的最小值为( )
如图,在△ACB中,有一点P在AC上移动,若AB=AC=5,BC=6,则AP+BP+CP的最小值为( )| A. | 4.8 | B. | 8 | C. | 8.8 | D. | 9.8 |
3.把分式$\frac{2x}{2x-3y}$中的x和y都扩大为原来的5倍,那么这个分式的值( )
| A. | 扩大为原来的5倍 | B. | 不变 | ||
| C. | 缩小到原来的$\frac{1}{5}$ | D. | 扩大为原来的$\frac{5}{2}$倍 |
 如图,在直线l上找一点P,使得PA+PB的和最小,并简要说明理由.(保留作图痕迹)
如图,在直线l上找一点P,使得PA+PB的和最小,并简要说明理由.(保留作图痕迹) 如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是$\sqrt{7}$.
如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是$\sqrt{7}$.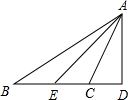 如图,在△ABC中,∠B=25°,∠ACB=105°,AD⊥BC,交BC的延长线于点D,AE平分∠BAC,求∠DAE的度数.
如图,在△ABC中,∠B=25°,∠ACB=105°,AD⊥BC,交BC的延长线于点D,AE平分∠BAC,求∠DAE的度数.