题目内容
10．一个正多边形的内角和与外角和相等，则该正多边形是正方形．分析 设此正多边形边数为n，根据内角和=外角和可得方程180（n-2）=360，再解即可．
解答 解：设此正多边形边数为n，由题意得：
180（n-2）=360，
解得：n=4，
故答案为：正方形．
点评 此题主要考查了多边形的内角和与外角和，关键是掌握多边形内角和定理：（n-2）•180° （n≥3）且n为整数），多边形的外角和等于360度．
练习册系列答案
相关题目
20．某年级学生共有246人，其中男生人数y比女生人数x的2倍多2人，则下面所列的方程组中符合题意的是（ ）
| A． | $\left\{\begin{array}{l}{x+y=246}\\{2y=x-2}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x+y=246}\\{2x=y+2}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{x+y=246}\\{y=2x+2}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x+y=246}\\{2y=x+2}\end{array}\right.$ |
18．
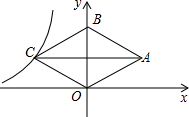如图，菱形OABC的顶点O是原点，顶点B在y轴上，菱形的两条对角线的长分别是6和4，反比例函数y=$\frac{k}{x}$（x＜0）的图象经过点C，则k的值为（ ）
如图，菱形OABC的顶点O是原点，顶点B在y轴上，菱形的两条对角线的长分别是6和4，反比例函数y=$\frac{k}{x}$（x＜0）的图象经过点C，则k的值为（ ）| A． | -12 | B． | -6 | C． | 6 | D． | 12 |
如图，将三角形的直角顶点放在直尺的一边上，若∠1=65°，则∠2的度数为25°．
20．甲乙两地相距75千米，从甲地到乙地货车所用时间比小车所用时间多15分钟，已知小车每小时比货车多行驶20千米，求两车的速度各为多少？设货车的速度为x千米/时，依题意列方程正确的是（ ）
| A． | $\frac{75}{x}=\frac{75}{x-20}+\frac{1}{4}$ | B． | $\frac{75}{x-20}=\frac{75}{x}+\frac{1}{4}$ | C． | $\frac{75}{x}=\frac{75}{x+20}-\frac{1}{4}$ | D． | $\frac{75}{x+20}=\frac{75}{x}-\frac{1}{4}$ |