题目内容
同学聚餐,每两人都要握手一次,若所有人共握手55次,那么参加聚餐的共有多少人?
考点:一元二次方程的应用
专题:应用题
分析:设参加聚餐的共有x人,根据每两人都要握手一次,若所有人共握手55次列出方程,求出方程的解即可得到结果.
解答:解:设参加聚餐的共有x人,
根据题意得:
=55,
即(x-11)(x+10)=0,
解得:x=11或x=-10(舍去).
则参加聚餐的共有11人.
根据题意得:
| x(x-1) |
| 2 |
即(x-11)(x+10)=0,
解得:x=11或x=-10(舍去).
则参加聚餐的共有11人.
点评:此题考查了一元二次方程的应用,弄清握手问题的实质是解本题的关键.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案
相关题目
下列命题中,是假命题的是( )
| A、同弧所对的圆周角相等 |
| B、同圆中相等的圆周角所对的弧相等 |
| C、等弧所对的圆周角相等或互补 |
| D、同圆中等弦所对的圆周角相等 |
解方程组
,以下解法不正确的是( )
|
| A、由①,②消去z,再由①,③消去z |
| B、由①,③消去z,再由②,③消去z |
| C、由①,③消去y,再由①,②消去y |
| D、由①,②消去z,再由①,③消去y |
 用边长为1的正方形纸片剪刀出一副七巧板,将其拼成如图的“小天鹅”,则阴影部分的面积是原正方形面积的
用边长为1的正方形纸片剪刀出一副七巧板,将其拼成如图的“小天鹅”,则阴影部分的面积是原正方形面积的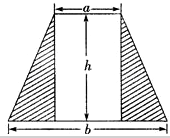 (1)用代数式表示图中阴影部分的面积S.
(1)用代数式表示图中阴影部分的面积S.