题目内容
17.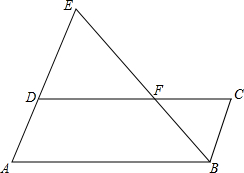 如图,F是?ABCD的边CD上一点,连接B对延长交AD的延长线于E.求证:$\frac{ED}{DA}=\frac{DF}{FC}$.
如图,F是?ABCD的边CD上一点,连接B对延长交AD的延长线于E.求证:$\frac{ED}{DA}=\frac{DF}{FC}$.
分析 由四边形ABCD是平行四边形,得到AD∥BC,AB∥CD,根据平行线分线段成比例得到$\frac{ED}{DA}$=$\frac{EF}{BF}$,通过△DEF∽△CBF,得到$\frac{EF}{BF}=\frac{DF}{CF}$,等量代换即可得到结论.
解答 证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴$\frac{ED}{DA}$=$\frac{EF}{BF}$,
∵AE∥BC,
∴△DEF∽△CBF,
∴$\frac{EF}{BF}=\frac{DF}{CF}$,
∴$\frac{ED}{DA}=\frac{DF}{FC}$.
点评 本题考查了平行四边形的性质,相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
 如图,把图形补成关于直线l对称的图形.
如图,把图形补成关于直线l对称的图形.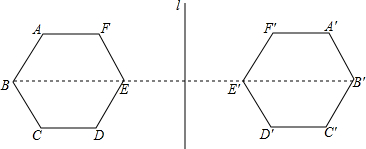
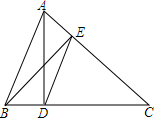 如图:AD和BE是锐角三角形ABC边BC、AC的两条高,垂足分别是点D和点E,若AC=6,CD=4,AB=5,求DE的长.
如图:AD和BE是锐角三角形ABC边BC、AC的两条高,垂足分别是点D和点E,若AC=6,CD=4,AB=5,求DE的长.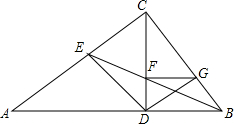 如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,∠ABC平分线交边AC于点E,交CD于F,过点F作FG∥AB,交边BC于点G,连结ED,GD.求证:$\frac{CE}{CD}$=$\frac{BG}{BD}$.
如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,∠ABC平分线交边AC于点E,交CD于F,过点F作FG∥AB,交边BC于点G,连结ED,GD.求证:$\frac{CE}{CD}$=$\frac{BG}{BD}$. ___________
___________