题目内容
2.(1)已知:a+b=3,ab=2.求a2+b2的值.(2)已知:a-b=1,a2+b2=4,求ab的值.
分析 (1)依据a2+b2=(a+b)2-2ab求解即可;
(2)依据2ab=(a2+b2)-(a-b)2求解即可.
解答 解:(1)a2+b2=(a+b)2-2ab=32-2×2=5;
(2)2ab=(a2+b2)-(a-b)2=4-1=3.
∴ab=1.5.
点评 本题主要考查的是完全平方公式的应用,应用公式进行适当变形是解题的关键.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
12.已知直角三角形ABC中,斜边AB的长为m,∠B=50°,则直角边BC的长是( )
| A. | msin50° | B. | mtan50° | C. | mcos50° | D. | $\frac{m}{{tan{{50}°}}}$ |
13.抛物线y=-(x-2)2向右平移2个单位得到的抛物线的解析式为( )
| A. | y=-x2 | B. | y=-(x-4)2 | C. | y=-(x-2)2+2 | D. | y=-(x-2)2-2 |
10.计算12÷(-3)-2×(-3)之值( )
| A. | -18 | B. | -10 | C. | 2 | D. | 18 |
7.若分式$\frac{x+2}{x-1}$的值为0,则x的值为( )
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
1.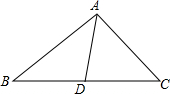 如图,在△ABC中,AB=7,BC边上的中线AD的长为5,则AC的长可能是( )
如图,在△ABC中,AB=7,BC边上的中线AD的长为5,则AC的长可能是( )
 如图,在△ABC中,AB=7,BC边上的中线AD的长为5,则AC的长可能是( )
如图,在△ABC中,AB=7,BC边上的中线AD的长为5,则AC的长可能是( )| A. | 3 | B. | 10 | C. | 17 | D. | 20 |
