Question

如图，⊙O的直径AB=4，∠ABC=30°，BC交⊙O于D，D是BC的中点．

（1）求BC的长；

（2）过点D作DE⊥AC，垂足为E，求证：直线DE是⊙O的切线．

 

Answer 1

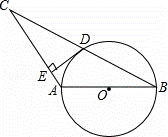
证明：（1）解：连接AD，

∵AB是⊙O的直径，

∴∠ADB=90°，

又∵∠ABC=30°，AB=4，

∴BD=2，

∵D是BC的中点，

∴BC=2BD=4；

（2）证明：连接OD．

∵D是BC的中点，O是AB的中点，

∴DO是△ABC的中位线，

∴OD∥AC，则∠EDO=∠CED

又∵DE⊥AC，

∴∠CED=90°，∠EDO=∠CED=90°

∴DE是⊙O的切线．