题目内容
在△AOB中,C,D分别是OA,OB边上的点,将△OCD绕点O顺时针旋转到△OC′D′.
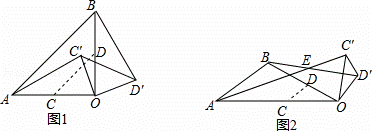
(1)如图1,若∠AOB=90°,OA=OB,C,D分别为OA,OB的中点,证明:①AC′=BD′;②AC′⊥BD′;
(2)如图2,若△AOB为任意三角形且∠AOB=θ,CD∥AB,AC′与BD′交于点E,猜想∠AEB=θ是否成立?请说明理由.
(1)证明:①∵△OCD旋转到△OC′D′,
∴OC=OC′,OD=OD′,∠AOC′=∠BOD′,
∵OA=OB,C、D为OA、OB的中点,
∴OC=OD,
∴OC′=OD′,
在△AOC′和△BOD′中, ,
,
∴△AOC′≌△BOD′(SAS),
∴AC′=BD′;
②延长AC′交BD′于E,交BO于F,如图1所示:
∵△AOC′≌△BOD′,
∴∠OAC′=∠OBD′,
又∠AFO=∠BFE,∠OAC′+∠AFO=90°,
∴∠OBD′+∠BFE=90°,
∴∠BEA=90°,
∴AC′⊥BD′;
(2)解:∠AEB=θ成立,理由如下:如图2所示:
∵△OCD旋转到△OC′D′,
∴OC=OC′,OD=OD′,∠AOC′=∠BOD′,
∵CD∥AB,
∴ ,
,
∴ ,
,
∴ ,
,
又∠AOC′=∠BOD′,
∴△AOC′∽△BOD′,
∴∠OAC′=∠OBD′,
又∠AFO=∠BFE,
∴∠AEB=∠AOB=θ.



 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=50°,则∠2的度数为( )

|
| A. | 50° | B. | 40° | C. | 30° | D. | 25° |
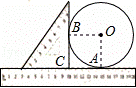
如图,圆形铁片与直角三角尺、直尺紧靠在一起平放在桌面上.已知铁片的圆心为O,三角尺的直角顶点C落在直尺的10cm处,铁片与直尺的唯一公共点A落在直尺的14cm处,铁片与三角尺的唯一公共点为B,下列说法错误的是( )
|
| A. | 圆形铁片的半径是4cm | B. | 四边形AOBC为正方形 |
|
| C. | 弧AB的长度为4πcm | D. | 扇形OAB的面积是4πcm2 |
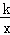 (k<0)的图象与矩形ABCD的边相交于E、F两点,且BE=2AE,E(﹣1,2).
(k<0)的图象与矩形ABCD的边相交于E、F两点,且BE=2AE,E(﹣1,2).
 的图象有一支位于第一象限,则常数a的取值范围是
的图象有一支位于第一象限,则常数a的取值范围是