题目内容
已知,在等腰△ABC中,AB=AC,∠BAC=a°,点K在△ABC内,且∠AKB=90°,将△ABK绕点A逆时针旋转a°,得△ACK′,作直线KK′交BC于点D,试探索CD与BD关系.
考点:圆的综合题,四点共圆,三角形内角和定理,三角形的外角性质,等腰三角形的性质,旋转的性质
专题:探究型
分析:连接AD,由旋转的性质可得AK=AK′,∠KAK′=a°,根据三角形内角和定理可求出∠AKK′,根据平角的定义可求出∠BKD;设∠BAK=b°,可求出∠BKD,然后根据三角形外角的性质可证到∠KDC=∠BAK,从而得到A、B、D、K四点共圆,根据圆周角定理就可得到∠ADB=∠AKB=90°,即AD⊥BC,再根据等腰三角形的性质就可得到CD与BD关系.
解答:解:连接AD,如图所示.
∵将△ABK绕点A逆时针旋转a°得到△ACK′,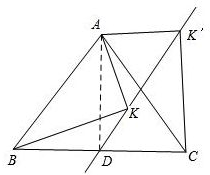
∴AK=AK′,∠KAK′=a°,
∠AKK′=∠AK′K=
=90°-
.
∵∠AKB=90°,
∴∠BKD=180°-90°-(90°-
)=
.
设∠BAK=b°,
∵∠AKB=90°,
∴∠ABK=90°-b°.
∵AB=AC,∠BAC=a°,
∴∠ABC=∠ACB=
=90°-
,
∴∠KBC=∠ABC-∠ABK=(90°-
)-(90°-b°)=b°-
.
∴∠KDC=∠BKD+∠KBC=
+b°-
=b°,
∴∠KDC=∠BAK,
∴A、B、D、K四点共圆,
∴∠ADB=∠AKB=90°,即AD⊥BC.
∵AB=AC,
∴BD=CD.
∵将△ABK绕点A逆时针旋转a°得到△ACK′,

∴AK=AK′,∠KAK′=a°,
∠AKK′=∠AK′K=
| 180°-a° |
| 2 |
| a° |
| 2 |
∵∠AKB=90°,
∴∠BKD=180°-90°-(90°-
| a° |
| 2 |
| a° |
| 2 |
设∠BAK=b°,
∵∠AKB=90°,
∴∠ABK=90°-b°.
∵AB=AC,∠BAC=a°,
∴∠ABC=∠ACB=
| 180°-a° |
| 2 |
| a° |
| 2 |
∴∠KBC=∠ABC-∠ABK=(90°-
| a° |
| 2 |
| a° |
| 2 |
∴∠KDC=∠BKD+∠KBC=
| a° |
| 2 |
| a° |
| 2 |
∴∠KDC=∠BAK,
∴A、B、D、K四点共圆,
∴∠ADB=∠AKB=90°,即AD⊥BC.
∵AB=AC,
∴BD=CD.
点评:本题考查了旋转的性质、四点共圆的判定、圆周角定理、等腰三角形的性质、三角形内角和定理、三角形的外角性质等知识,有一定的综合性,而证明A、B、D、K四点共圆则是解决本题的关键.

练习册系列答案
相关题目
下列说法正确的是( )
| A、自然数就是非负整数 |
| B、一个数不是正数,就是负数 |
| C、整数就是自然数 |
| D、正数和负数统称有理数 |
 如图,AB∥CD,AB=AC,BF∥AE,点P是直线BF上一点,点Q是直线CD上一点,∠PAQ=∠EAB.求证:AP=AQ.
如图,AB∥CD,AB=AC,BF∥AE,点P是直线BF上一点,点Q是直线CD上一点,∠PAQ=∠EAB.求证:AP=AQ.
 如图,已知AC=AD,BC=BD,E为AB上一点,试证明∠CEB=∠DEB.
如图,已知AC=AD,BC=BD,E为AB上一点,试证明∠CEB=∠DEB.