题目内容
10. 如图,四边形ABCD是⊙O的内接四边形,AB是⊙O的直径,∠D=124°,MN切⊙O于点C,求∠BCM的度数.
如图,四边形ABCD是⊙O的内接四边形,AB是⊙O的直径,∠D=124°,MN切⊙O于点C,求∠BCM的度数.
分析 连结OC,如图,根据内接四边形的性质得到∠B=180°-∠D=56°,则∠OCB=∠B=56°,再根据切线的性质得∠OCM=90°,然后利用互余计算∠BCM的度数.
解答 解:连结OC,如图,
∵四边形ABCD是⊙O的内接四边形,
∴∠B=180°-∠D=180°-124°=56°,
∵OB=OC,
∴∠OCB=∠B=56°,
∵MN切⊙O于点C,
∴OC⊥MN,
∴∠OCM=90°,
∴∠BCM=90°-∠OCB=90°-56°=34°.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了圆内接四边形的性质.

练习册系列答案
相关题目
20.下列两个变量之间不存在函数关系的是( )
| A. | 圆的面积S和半径R之间的关系 | |
| B. | 匀速行驶的汽车,行驶的路程s与时间t之间的关系 | |
| C. | 一个正数的平方根与它本身之间的关系 | |
| D. | 电阻一定,加在这个电阻两端的电压通过这个电阻的电流之间的关系 |
 八年级(6)班的同学做游戏,在活动区放了一些球(如图),小明应按怎样的路线跑,去捡起那个位置的球,才能最快拿到球跑到目的地A?
八年级(6)班的同学做游戏,在活动区放了一些球(如图),小明应按怎样的路线跑,去捡起那个位置的球,才能最快拿到球跑到目的地A?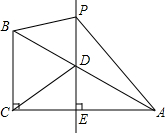 如图,在△ABC中,当∠ACB=90°,∠BAC=30°,BC=$\sqrt{3}$,过AB的中点D作DE⊥AC,垂足为点E,点P是直线DE上一动点,连结AP,BP,CD
如图,在△ABC中,当∠ACB=90°,∠BAC=30°,BC=$\sqrt{3}$,过AB的中点D作DE⊥AC,垂足为点E,点P是直线DE上一动点,连结AP,BP,CD 的解集为
的解集为 ,则
,则 的取值范围是 __________
的取值范围是 __________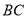 ∥
∥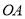 ,
, 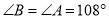 ,试解答下列问题:
,试解答下列问题: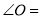 __________,则OB与AC的位置关系为__________
__________,则OB与AC的位置关系为__________
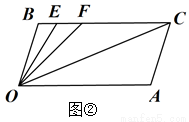
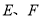 在线段
在线段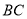 上,且满足
上,且满足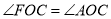 ,并且
,并且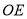 平分
平分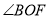 .则
.则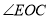 的度数等于_____________;
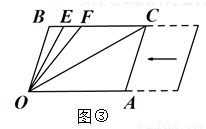
的度数等于_____________;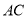 到如图③所示位置.
到如图③所示位置.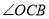 与
与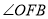 的比值是否发生改变,若不改变求出其比值,若要改变说明理由;
的比值是否发生改变,若不改变求出其比值,若要改变说明理由;