题目内容
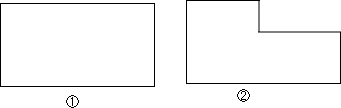
2.如图①,将一张矩形纸片沿直线折叠一次,折痕恰好把矩形分成面积相等的两部分.(1)这样的折痕有无数条,这些折痕具有的特点是过矩形对称中心;
(2)请将图②中方角形余料用一条直线分成面积相等的两部分.
分析 (1)由将一张矩形纸片沿直线折叠一次,折痕恰好把矩形分为面积相等的两部分的直线有无数条,即可得这样的折痕有无数条;由矩形的性质,即可证得这样的折痕具有的特点为:过矩形对称中心;
(2)将已知图形分割为两个矩形,进而连接两矩形的中心得出即可.
解答 解:(1)如图1所示: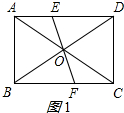 无数条;这些折痕具有的特点是过矩形对称中心;
无数条;这些折痕具有的特点是过矩形对称中心;
理由:∵四边形ABCD是矩形,
∴OA=OC,OB=OD,AD∥BC,AB∥CD,
∴∠EAO=∠FCO,∠AEO=∠CFO,
在△AOE和△COF中,$\left\{\begin{array}{l}{∠EAO=∠FCO}\\{∠AEO=∠CFO}\\{OA=OC}\end{array}\right.$,
∴△AOE≌△COF(AAS)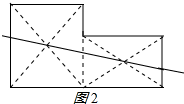
同理:△EOD≌△FOB,△AOB≌△COD,
∴S△AOE+S△AOB+S△BOF=S△COF+S△COD+S△DOE.
∴这样的折痕具有的特点为:过矩形对称中心;
故答案为:无数,过矩形对称中心;
(2)把方角形余料分成两个矩形,过两个矩形对称中心作直线,
把方角形余料分成面积相等的两部分,如图2所示.
点评 此题主要考查了矩形的性质、全等三角形的判定与性质、应用设计与作图以及中心对称的性质;得出平分中心对称图形的方法是解题关键.

练习册系列答案
相关题目
12.把-(-18)-(+7)-(-4)+(-2)写成省略加号的和的形式为( )
| A. | 18-7+4-2 | B. | 18+7-4-2 | C. | -18-7+4-2 | D. | -18-7-4-2 |
13. 2015年9月19日第九届合肥文博会开幕.开幕前夕,我市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销.经过调查,得到如下数据:
2015年9月19日第九届合肥文博会开幕.开幕前夕,我市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销.经过调查,得到如下数据:
(1)把上表中x、y的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想y与x的函数关系,并求出函数关系式;
(2)当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?
(3)开幕后,合肥市物价部门规定,该工艺品销售单价最高不能超过38元/件,那么销售单价定为多少时,工艺厂销售该工艺品每天获得的利润最大?最大利润是多少?
 2015年9月19日第九届合肥文博会开幕.开幕前夕,我市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销.经过调查,得到如下数据:
2015年9月19日第九届合肥文博会开幕.开幕前夕,我市某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销.经过调查,得到如下数据:| 销售单价x(元/件) | … | 20 | 30 | 40 | 50 | 60 | … |
| 每天销售量(y件) | … | 500 | 400 | 300 | 200 | 100 | … |
(2)当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?
(3)开幕后,合肥市物价部门规定,该工艺品销售单价最高不能超过38元/件,那么销售单价定为多少时,工艺厂销售该工艺品每天获得的利润最大?最大利润是多少?
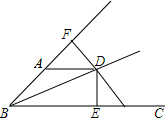 如图,已知BD为∠ABC的平分线,DE⊥BC于E,DF⊥BA于F,且AD=DC.
如图,已知BD为∠ABC的平分线,DE⊥BC于E,DF⊥BA于F,且AD=DC. 问题探究:观察下面由“※”组成的图案和算式,解答问题:
问题探究:观察下面由“※”组成的图案和算式,解答问题: