题目内容
17.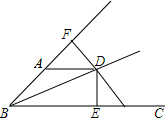 如图,已知BD为∠ABC的平分线,DE⊥BC于E,DF⊥BA于F,且AD=DC.
如图,已知BD为∠ABC的平分线,DE⊥BC于E,DF⊥BA于F,且AD=DC.求证:∠BAD+∠BCD=180°.
分析 先由角平分线性质得出DE=DF,再证明Rt△BFD≌Rt△BED即可.
解答 解:如图,
∵BD为∠ABC的平分线,DE⊥BC,DF⊥BA,
∴DF=DE,
Rt△BFD和Rt△BED中,
$\left\{\begin{array}{l}{AD=DC}\\{DF=DE}\end{array}\right.$,
∴Rt△BFD≌Rt△BED (HL),
∴∠DCE=∠FAD,
∵∠BAD+∠FAD=180°,
∴∠BAD+∠BCD=180°.
点评 本题主要考查了角平分线的线性质、全等三角形的判定与性质,难度不大.对于全等三角形的判定,找准对应的相等角和相等边是关键.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
7.下列叙述正确的是( )
| A. | 近似数8.96×104精确到百分位 | B. | 近似数5.3万精确到千位 | ||
| C. | 近似数0.310有两个有效数字 | D. | 用科学记数法表示80500=8.05×105 |
 如图,OP平分∠MON,PE⊥OM于E,PF⊥ON于F,OA=OB,则图中全等三角形的对数为( )
如图,OP平分∠MON,PE⊥OM于E,PF⊥ON于F,OA=OB,则图中全等三角形的对数为( )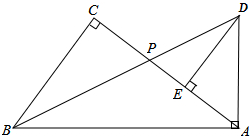 如图,在Rt△ABC中,∠C=90°,点P为AC边上的一点,延长BP至点D,使得AD=AP,当AD⊥AB时,过点D作DE⊥AC于E.
如图,在Rt△ABC中,∠C=90°,点P为AC边上的一点,延长BP至点D,使得AD=AP,当AD⊥AB时,过点D作DE⊥AC于E. 如图,AB是半圆O的直径,E是弧BC的中点,OE交弦BC于点D,已知BC=8,DE=2,求圆O的半径的长.
如图,AB是半圆O的直径,E是弧BC的中点,OE交弦BC于点D,已知BC=8,DE=2,求圆O的半径的长.
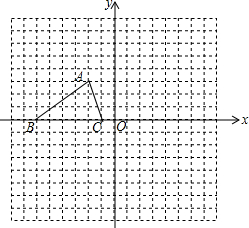 如图,已知△ABC三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).
如图,已知△ABC三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).