题目内容
10.(1)($\sqrt{10}$-3)2014($\sqrt{10}$+3)2013=$\sqrt{10}$-3(2)(1$+\sqrt{3}$)(3-$\sqrt{3}$)=2$\sqrt{3}$.
分析 (1)先利用积的乘方得到原式=($\sqrt{10}$-3)[($\sqrt{10}$-3)($\sqrt{10}$+3)]2013,然后根据平方差公式计算;
(2)先把后面括号内提$\sqrt{3}$,然后利用平方差公式计算.
解答 解:(1)原式=($\sqrt{10}$-3)[($\sqrt{10}$-3)($\sqrt{10}$+3)]2013
=($\sqrt{10}$-3)(10-9)2013
=$\sqrt{10}$-3;
(2)原式=($\sqrt{3}$+1)•$\sqrt{3}$($\sqrt{3}$-1)
=(3-1)•$\sqrt{3}$
=2$\sqrt{3}$.
故答案为$\sqrt{10}$-3,2$\sqrt{3}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
相关题目
15.已知一个等腰三角形两内角的度数之比为1:2,则这个等腰三角形底角的度数为( )
| A. | 72° | B. | 45° | C. | 45°或72° | D. | 60° |
20.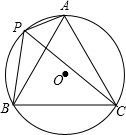 如图,A、B、C、P是⊙O上的四个点,∠ACB=60°,且PC平分∠APB,则△ABC的形状是( )
如图,A、B、C、P是⊙O上的四个点,∠ACB=60°,且PC平分∠APB,则△ABC的形状是( )
 如图,A、B、C、P是⊙O上的四个点,∠ACB=60°,且PC平分∠APB,则△ABC的形状是( )
如图,A、B、C、P是⊙O上的四个点,∠ACB=60°,且PC平分∠APB,则△ABC的形状是( )| A. | 直角三角形 | B. | 等腰三角形 | C. | 等边三角形 | D. | 等腰直角三角形 |
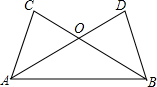 已知:如图,AD、BC相交于点O,OA=OB,∠C=∠D.
已知:如图,AD、BC相交于点O,OA=OB,∠C=∠D.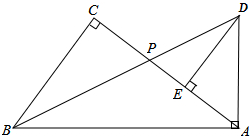 如图,在Rt△ABC中,∠C=90°,点P为AC边上的一点,延长BP至点D,使得AD=AP,当AD⊥AB时,过点D作DE⊥AC于E.
如图,在Rt△ABC中,∠C=90°,点P为AC边上的一点,延长BP至点D,使得AD=AP,当AD⊥AB时,过点D作DE⊥AC于E.