题目内容
20.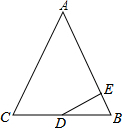 如图,在△ABC中,AB=AC=13,BC=10,点D为BC的中点,DE⊥AB于点E,则tan∠BDE的值等于( )
如图,在△ABC中,AB=AC=13,BC=10,点D为BC的中点,DE⊥AB于点E,则tan∠BDE的值等于( )| A. | $\frac{10}{13}$ | B. | $\frac{13}{10}$ | C. | $\frac{5}{12}$ | D. | $\frac{12}{5}$ |
分析 连接AD,由△ABC中,AB=AC=13,BC=10,D为BC中点,利用等腰三角形三线合一的性质,可证得AD⊥BC,再利用勾股定理,求得AD的长,那么在直角△ABD中根据三角函数的定义求出tan∠BAD,然后根据同角的余角相等得出∠BDE=∠BAD,于是tan∠BDE=tan∠BAD.
解答  解:连接AD,
解:连接AD,
∵△ABC中,AB=AC=13,BC=10,D为BC中点,
∴AD⊥BC,BD=$\frac{1}{2}$BC=5,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=12,
∴tan∠BAD=$\frac{BD}{AD}$=$\frac{5}{12}$.
∵AD⊥BC,DE⊥AB,
∴∠BDE+∠ADE=90°,∠BAD+∠ADE=90°,
∴∠BDE=∠BAD,
∴tan∠BDE=tan∠BAD=$\frac{5}{12}$.
故选C.
点评 此题考查了解直角三角形、等腰三角形的性质、勾股定理、锐角三角函数的定义以及余角的性质.此题难度适中,解题的关键是准确作出辅助线,注意数形结合思想的应用.

练习册系列答案
相关题目
5.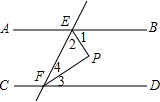 如图,已知AB∥CD,∠1=∠2,EP⊥FP,则以下正确的是( )
如图,已知AB∥CD,∠1=∠2,EP⊥FP,则以下正确的是( )
 如图,已知AB∥CD,∠1=∠2,EP⊥FP,则以下正确的是( )
如图,已知AB∥CD,∠1=∠2,EP⊥FP,则以下正确的是( )| A. | ∠3=∠4 | B. | ∠2+∠4=180° | C. | ∠1与∠2互余 | D. | ∠1=∠3 |
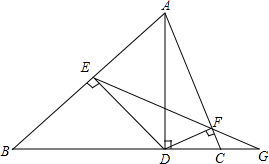 已知AD是△ABC的高,点D在BC内,且BD=3,CD=1,作DE⊥AB于点E,DF⊥AC于点F,连接EF并延长,交BC的延长线于点G,求CG.
已知AD是△ABC的高,点D在BC内,且BD=3,CD=1,作DE⊥AB于点E,DF⊥AC于点F,连接EF并延长,交BC的延长线于点G,求CG.
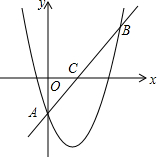 在平面直角坐标系中,抛物线y=2x2+bx+c经过点A(0,-2),B(3,4).
在平面直角坐标系中,抛物线y=2x2+bx+c经过点A(0,-2),B(3,4).