题目内容
9.如图,在平面直角坐标系中,点A(10,0)和点B(0,2.5)在线段OA上,点P从点O向点A运动,同时点Q从点A向点O运动,运动过程中保持AQ=2OP,当P,Q重合时同时停止运动,过点Q作x轴的垂线,交直线AB于点M,延长QM到点D,使MD=MQ,以QD为对角线作正方形QCDE.过点P作x轴的垂线,交直线AB于点N,延长PN到点G,使NG=PN,以PG为对角线作正方形PFGH(正方形EQCD,PFGH随点Q,P运动),当OP=2或2.5时,正方形PFGH的边和正方形QCDE的边落在同一条直线上.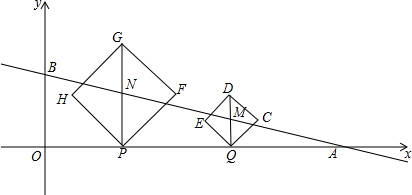
分析 先求得直线AB的解析式然后分两种情况:①当GF和EQ落在同一条直线上时,△PGQ为等腰直角三角形,设OP=a,PQ=b,根据等腰直角三角形的性质PG=PQ=b,由于点N在直线AB上,得出$\frac{b}{2}$=-0.25a+2.5,由AQ=2OP,得出AQ=2a,因为OQ=a+b,OQ+AQ=OA=10,得出2a+a+b=10,从而求得OP=2,②当PF和ED落在同一条直线上时,△PEQ为等腰直角三角形,得出PQ=DQ=b,M(a+b,$\frac{b}{2}$),由于点M在直线AB上,得出$\frac{b}{2}$=-0.25(a+b)+2.5,求得b=$\frac{-a+10}{3}$,根据2a+a+b=10,解得a=2.5.
解答  解:设直线AB的解析式为y=kx+b,
解:设直线AB的解析式为y=kx+b,
∵点A(10,0)和点B(0,2.5),
∴$\left\{\begin{array}{l}{10k+b=0}\\{b=2.5}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-0.25}\\{b=2.5}\end{array}\right.$,
∴直线AB的解析式为y=-0.25x+2.5,
①当GF和EQ落在同一条直线上时,△PGQ为等腰直角三角形,如图1,
设OP=a,PQ=b,
∴PG=PQ=b,OQ=a+b,
∵点N在直线AB上,
∴$\frac{b}{2}$=-0.25a+2.5,
∵AQ=2OP,
∴AQ=2a,
∵OQ+AQ=OA=10,
∴2a+a+b=10,
∴3a+2(-0.25a+2.5)=10,解得a=2,
∴OP=2,
②当PF和ED落在同一条直线上时,△PEQ为等腰直角三角形,如图2,
∴PQ=DQ=b,
∴M(a+b,$\frac{b}{2}$),
∵点M在直线AB上,
∴$\frac{b}{2}$=-0.25(a+b)+2.5,
∴b=$\frac{-a+10}{3}$,
∵2a+a+b=10,
∴3a+$\frac{-a+10}{3}$=10,解得a=2.5;
故当OP=2或2.5时,正方形PFGH的边和正方形QCDE的边落在同一条直线上.
故答案为2或2.5.
点评 本题考查了一次函数的综合运用.关键是根据正方形对角线的性质及其与x轴垂直解题.

 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案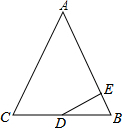 如图,在△ABC中,AB=AC=13,BC=10,点D为BC的中点,DE⊥AB于点E,则tan∠BDE的值等于( )
如图,在△ABC中,AB=AC=13,BC=10,点D为BC的中点,DE⊥AB于点E,则tan∠BDE的值等于( )| A. | $\frac{10}{13}$ | B. | $\frac{13}{10}$ | C. | $\frac{5}{12}$ | D. | $\frac{12}{5}$ |
| A. | 2x5 | B. | 2x | C. | 2x6 | D. | x5 |
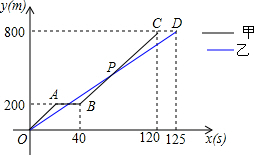 在800米跑步测试过程中,甲乙两名运动员同时起跑,刚跑出200米时甲不慎摔倒,他又迅速爬起来再次投入比赛,并最终超越乙取得优异成绩.图中分别表示甲、乙两名运动员所跑的路程y(m)与比赛时间x(s)之间的关系.
在800米跑步测试过程中,甲乙两名运动员同时起跑,刚跑出200米时甲不慎摔倒,他又迅速爬起来再次投入比赛,并最终超越乙取得优异成绩.图中分别表示甲、乙两名运动员所跑的路程y(m)与比赛时间x(s)之间的关系.