题目内容
10.已知:x=$\sqrt{3}$+$\sqrt{2}$,y=$\sqrt{3}$-$\sqrt{2}$,求代数式x2-y2+5xy的值.分析 首先把代数式利用平方差公式因式分解,再进一步代入求得答案即可.
解答 解:∵x=$\sqrt{3}$+$\sqrt{2}$,y=$\sqrt{3}$-$\sqrt{2}$,
∴x2-y2+5xy
=(x+y)(x-y)+5xy
=2$\sqrt{3}$×2$\sqrt{2}$+5($\sqrt{3}$+$\sqrt{2}$)($\sqrt{3}$-$\sqrt{2}$)
=4$\sqrt{6}$+5.
点评 此题考查二次根式的化简求值,根据数据特点,灵活变形,进一步代入求得答案即可.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
20.如果关于x的一元二次方程x2+px+q=0的两根分别为x1=-3,x2=2,那么p、q的值分别是( )
| A. | 1,-6 | B. | -1,-6 | C. | -1,6 | D. | 1,6 |
5.下列标志中,可以看作是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
2. 用两块相同的三角板按如图所示的方式作平行线AB和CD,能解释其中的道理的依据是( )
用两块相同的三角板按如图所示的方式作平行线AB和CD,能解释其中的道理的依据是( )
 用两块相同的三角板按如图所示的方式作平行线AB和CD,能解释其中的道理的依据是( )
用两块相同的三角板按如图所示的方式作平行线AB和CD,能解释其中的道理的依据是( )| A. | 内错角相等,两直线平行 | B. | 同位角相等,两直线平行 | ||
| C. | 同旁内角互补,两直线平行 | D. | 平行于同一直线的两直线平行 |
20.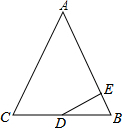 如图,在△ABC中,AB=AC=13,BC=10,点D为BC的中点,DE⊥AB于点E,则tan∠BDE的值等于( )
如图,在△ABC中,AB=AC=13,BC=10,点D为BC的中点,DE⊥AB于点E,则tan∠BDE的值等于( )
 如图,在△ABC中,AB=AC=13,BC=10,点D为BC的中点,DE⊥AB于点E,则tan∠BDE的值等于( )
如图,在△ABC中,AB=AC=13,BC=10,点D为BC的中点,DE⊥AB于点E,则tan∠BDE的值等于( )| A. | $\frac{10}{13}$ | B. | $\frac{13}{10}$ | C. | $\frac{5}{12}$ | D. | $\frac{12}{5}$ |