题目内容
5.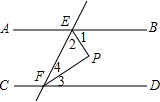 如图,已知AB∥CD,∠1=∠2,EP⊥FP,则以下正确的是( )
如图,已知AB∥CD,∠1=∠2,EP⊥FP,则以下正确的是( )| A. | ∠3=∠4 | B. | ∠2+∠4=180° | C. | ∠1与∠2互余 | D. | ∠1=∠3 |
分析 过点P作PE∥AB,再根据平行线的性质及直角三角形的性质对各选项进行逐一判断即可.
解答  解:过点P作PE∥AB,
解:过点P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD,
∴∠1=∠EPH,∠3=∠HPF,
∵EP⊥FP,
∴∠2+∠4=90°,∠HPF+∠EPH=90°,
∴∠3=∠4,故A正确;
∵EP⊥FP,
∴∠2+∠4=90°,故B错误;
∵∠1=∠2,∠3=∠4,∠2+∠4=90°,
∴∠1+∠3=90°,∠1与∠3互余,故C、D错误;
故选A.
点评 本题考查的是平行线的性质,根据题意作出辅助线,构造出平行线是解答此题的关键.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
16.计算100m•1000n的结果是( )
| A. | 100000m+n | B. | 100mn | C. | 1000mn | D. | 102m+3n |
13. 如图,在⊙O中,AC∥OB,∠BAO=25°,则∠BOC的度数为( )
如图,在⊙O中,AC∥OB,∠BAO=25°,则∠BOC的度数为( )
 如图,在⊙O中,AC∥OB,∠BAO=25°,则∠BOC的度数为( )
如图,在⊙O中,AC∥OB,∠BAO=25°,则∠BOC的度数为( )| A. | 80° | B. | 60° | C. | 50° | D. | 25° |
20.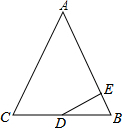 如图,在△ABC中,AB=AC=13,BC=10,点D为BC的中点,DE⊥AB于点E,则tan∠BDE的值等于( )
如图,在△ABC中,AB=AC=13,BC=10,点D为BC的中点,DE⊥AB于点E,则tan∠BDE的值等于( )
 如图,在△ABC中,AB=AC=13,BC=10,点D为BC的中点,DE⊥AB于点E,则tan∠BDE的值等于( )
如图,在△ABC中,AB=AC=13,BC=10,点D为BC的中点,DE⊥AB于点E,则tan∠BDE的值等于( )| A. | $\frac{10}{13}$ | B. | $\frac{13}{10}$ | C. | $\frac{5}{12}$ | D. | $\frac{12}{5}$ |