题目内容
6.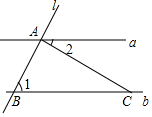 如图,直线a∥b,直线l与a、b分别相交于A、B两点,过点A作直线l的垂线交直线b于点C.若∠2=32°;则∠1的度数为( )
如图,直线a∥b,直线l与a、b分别相交于A、B两点,过点A作直线l的垂线交直线b于点C.若∠2=32°;则∠1的度数为( )| A. | 58° | B. | 42° | C. | 32° | D. | 28° |
分析 根据平行线的性质得出∠ACB=∠2,根据三角形内角和定理求出即可.
解答 解:∵直线a∥b,
∴∠ACB=∠2,
∵AC⊥BA,
∴∠BAC=90°,
∴∠2=∠ACB=180°-∠1-∠BAC=32°,
∴∠1=58°,
故选A.
点评 本题考查了对平行线的性质和三角形内角和定理的应用,注意:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
16.关于x的一元二次方程x2+4x-2k=0有两个实数根,则实数k的取值范围是( )
| A. | k≥-2 | B. | k≤-2 | C. | k>-2 | D. | k=-2 |
17.若a>1,则a,-a,$\frac{1}{a}$从大到小排列正确的是( )
| A. | a>-a>$\frac{1}{a}$ | B. | a>$\frac{1}{a}$>-a | C. | $\frac{1}{a}$>-a>a | D. | $\frac{1}{a}$>-a>a> |
14.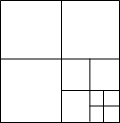 如图,连接边长为1的正方形对边中点,可将一个正方形分成4个大小相同的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成4个更小的小正方形…重复这样的操作,则5次操作后右下角的小正方形面积是( )
如图,连接边长为1的正方形对边中点,可将一个正方形分成4个大小相同的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成4个更小的小正方形…重复这样的操作,则5次操作后右下角的小正方形面积是( )
 如图,连接边长为1的正方形对边中点,可将一个正方形分成4个大小相同的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成4个更小的小正方形…重复这样的操作,则5次操作后右下角的小正方形面积是( )
如图,连接边长为1的正方形对边中点,可将一个正方形分成4个大小相同的小正方形,选右下角的小正方形进行第二次操作,又可将这个小正方形分成4个更小的小正方形…重复这样的操作,则5次操作后右下角的小正方形面积是( )| A. | ($\frac{1}{4}$)5 | B. | ($\frac{1}{2}$)5 | C. | $\frac{1}{5}$ | D. | 1-($\frac{1}{4}$)5 |
1.(-$\sqrt{3}$)2等于( )
| A. | -3 | B. | 3 | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
11.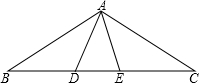 如图,∠ADB=∠AEC=100°,∠BAD=50°,BD=EC,则∠C=( )
如图,∠ADB=∠AEC=100°,∠BAD=50°,BD=EC,则∠C=( )
 如图,∠ADB=∠AEC=100°,∠BAD=50°,BD=EC,则∠C=( )
如图,∠ADB=∠AEC=100°,∠BAD=50°,BD=EC,则∠C=( )| A. | 20° | B. | 50° | C. | 30° | D. | 40° |
18.已知A(m,y1)和B(-2,y2)是函数y=-$\frac{6}{x}$上的点,且y1>y2,则m的取值范围是( )
| A. | -2<m<0 | B. | m>-2 | C. | m<-2 | D. | m<-2或m>0 |
15. 如图,在?ABCD中,CE⊥AB,∠A=130°,则∠BCE的度数为( )
如图,在?ABCD中,CE⊥AB,∠A=130°,则∠BCE的度数为( )
 如图,在?ABCD中,CE⊥AB,∠A=130°,则∠BCE的度数为( )
如图,在?ABCD中,CE⊥AB,∠A=130°,则∠BCE的度数为( )| A. | 80° | B. | 50° | C. | 40° | D. | 30° |
16.在一个布袋里装有白球6只、红球2只、黑球4只,它们除颜色外没有任何区别,从袋中随机取出1只球,则取出红球的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |