题目内容
2.如图,平行四边形ABCD的面积为36cm2,AB=9cm,∠A=45°,点P是线段AB上一点,AP=6cm,点G以每秒1cm的速度,从点P出发沿线段PA向点A作匀速运动,同时点F以每秒3cm的速度,从点P出发沿线段PA向点A作匀速运动,到达点A后按原路返回,与G点相遇时停止,设G,F运动的时间为t秒(t>0),正方形EFGH与平行四边形ABCD重叠部分的面积为s.(1)当t=1.5时,正方形EFGH的边长是3cm;
当t=2.5时,正方形EFGH的边长是2cm;
(2)当0<t≤2时,求S与t的函数关系式.

分析 (1)根据题意,可以分别求得PG、PF的长度,从而可以求得FG的长度,从而可以解答本题;
(2)根据题意可以分两种情况,然后针对不同的情况求出t的取值范围,从而可以表示出S与t的函数关系式.
解答 解:(1)由题意可得,
当t=1.5时,PG=1×1.5=1.5cm,PF=3×1.5=4.5cm,
故t=1.5时,FG=4.5-1.5=3cm;
当t=2.5时,PG=1×2.5=2.5,PF=6-(2.5×3-6)=4.5cm,
故t=2.5时,FG=4.5-2.5=2cm;
故答案为:3cm,2cm;
(2)∵平行四边形ABCD的面积为36cm2,AB=9cm,∠A=45°,点P是线段AB上一点,AP=6cm,
∴点D到AB的距离为:36÷9=4cm,
当点E恰好落在线段AD上时,此时PG=t,PF=3t,
∴EF=FG=3t-t=2t,
∴AF=EF=2t,
∴2t+3t=6,得t=1.2,
∴当0<t≤1.2时,S=(2t)2=4t2;
当1.2<t≤2时,S=4t2-$\frac{[2t-(6-3t)]^{2}}{2}$=-8.5t2+30t-18,
即S与t的函数关系式是:S=$\left\{\begin{array}{l}{4{t}^{2}}&{0<t≤1.2}\\{-8.5{t}^{2}+30t-18}&{1.2<t≤2}\end{array}\right.$.
点评 本题考查四边形综合题,解题的关键是明确题意,找出所求问题需要的条件,会求函数的解析式,运用分类讨论的数学思想解答问题.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
13.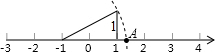 如图,数轴上的点A所表示的数为x,则x的值为( )
如图,数轴上的点A所表示的数为x,则x的值为( )
 如图,数轴上的点A所表示的数为x,则x的值为( )
如图,数轴上的点A所表示的数为x,则x的值为( )| A. | $\sqrt{5}$ | B. | $\sqrt{5}$+1 | C. | $\sqrt{5}$-1 | D. | 1-$\sqrt{5}$ |
10.下列命题中,真命题的是( )
| A. | 周长相等的锐角三角形都全等 | B. | 周长相等的直角三角形都全等 | ||
| C. | 周长相等的等腰直角三角形都全等 | D. | 周长相等的钝角三角形都全等 |
17.下列长度的三条线段:①3,8,4②4,9,6③15,20,8④9,15,8,其中能构成三角形的有( )
| A. | 4组 | B. | 3组 | C. | 2组 | D. | 1组 |
11. 如图,为测量池塘边上两点A,B之间的距离,小明在池塘的一侧选取一点O,取OA,OB的中点D,E,测出DE=12米,那么A,B间的距离是( )
如图,为测量池塘边上两点A,B之间的距离,小明在池塘的一侧选取一点O,取OA,OB的中点D,E,测出DE=12米,那么A,B间的距离是( )
 如图,为测量池塘边上两点A,B之间的距离,小明在池塘的一侧选取一点O,取OA,OB的中点D,E,测出DE=12米,那么A,B间的距离是( )
如图,为测量池塘边上两点A,B之间的距离,小明在池塘的一侧选取一点O,取OA,OB的中点D,E,测出DE=12米,那么A,B间的距离是( )| A. | 24米 | B. | 20米 | C. | 30米 | D. | 18米 |
 已知:如图,在菱形ABCD中,∠BCD=2∠ABC,AC=4,求菱形ABCD的周长.
已知:如图,在菱形ABCD中,∠BCD=2∠ABC,AC=4,求菱形ABCD的周长. 如图,?ABCD的对角线AC、BD相交于点O,AE=CF.
如图,?ABCD的对角线AC、BD相交于点O,AE=CF.