题目内容
20.解方程(1)2x2-9x+8=0
(2)5x2-2x-$\frac{1}{4}$=x2-2x+$\frac{3}{4}$.
分析 (1)先计算判别式的值,然后根据求根公式解方程;
(2)先把方程整理为4x2-1=0,然后利用因式分解法解方程.
解答 解:(1)△=(-9)2-4×2×8=17,
x=$\frac{9±\sqrt{17}}{2×2}$,
所以x1=$\frac{9+\sqrt{17}}{4}$,x2=$\frac{9-\sqrt{17}}{4}$;
(2)方程整理为4x2-1=0,
(2x+1)(2x-1)=0,
2x+1=0或2x-1=0,
所以x1=-$\frac{1}{2}$,x2=$\frac{1}{2}$.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了公式法解一元二次方程.

练习册系列答案
 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
15.方程13x-$\frac{1}{6}$(5x-4)=10x-8的解是( )
| A. | x=$\frac{36}{11}$ | B. | x=-$\frac{44}{13}$ | C. | x=-4 | D. | x=2 |
13.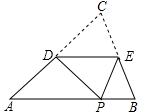 如图,D、E分别为△ABC的AC,BC边的中点,将此三角形沿DE折叠,若∠CDE=48°,则∠ADP等于( )
如图,D、E分别为△ABC的AC,BC边的中点,将此三角形沿DE折叠,若∠CDE=48°,则∠ADP等于( )
 如图,D、E分别为△ABC的AC,BC边的中点,将此三角形沿DE折叠,若∠CDE=48°,则∠ADP等于( )
如图,D、E分别为△ABC的AC,BC边的中点,将此三角形沿DE折叠,若∠CDE=48°,则∠ADP等于( )| A. | 42° | B. | 48° | C. | 84° | D. | 58° |