题目内容
9．已知：x2-6x+9与|y-2|互为相反数，则式子（$\frac{x}{y}$-$\frac{y}{x}$）÷（x+y）的值等于$\frac{1}{6}$．分析 根据x2-6x+9与|y-2|互为相反数，可以求得x、y的值，从而可以解答本题．
解答 解：∵x2-6x+9=（x-3）2，x2-6x+9与|y-2|互为相反数，
∴x-3=0，y-2=0．
得x=3，y=2．
∴（$\frac{x}{y}$-$\frac{y}{x}$）÷（x+y）
=$（\frac{3}{2}-\frac{2}{3}）÷（3+2）$
=$\frac{5}{6}×\frac{1}{5}$
=$\frac{1}{6}$．
故答案为：$\frac{1}{6}$．
点评 本题考查分式的化简求值，解题的关键是可以根据题意找出所求问题需要的条件．
练习册系列答案
相关题目
如图所示，有下列说法：（1）∠ECG和∠C是同一个角；（2）∠OGF和∠OGB是同一个角；（3）∠DOF和∠EOG是同一个角；（4）∠ABC和∠ACB是同一个角．其中，正确的有（ ）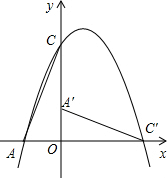
如图，在直角坐标系中，O是坐标原点，点C的坐标是（0，3），抛物线y=-x2+2x+c经过点C，交x轴负半轴于点A．