题目内容
 如图,Rt△ABC中,∠ACB=90°,BC=6,AB=10,以BC为直径的⊙O交AB于D,AC、DO的延长线交于E,点M为线段AC上一点,且CM=4.
如图,Rt△ABC中,∠ACB=90°,BC=6,AB=10,以BC为直径的⊙O交AB于D,AC、DO的延长线交于E,点M为线段AC上一点,且CM=4.(1)求证:直线DM是圆O的切线.
(2)求tan∠E的值.
考点:切线的判定
专题:证明题
分析:(1)连结CD,如图,先利用勾股定理计算出AC=8,则CM=AM=4,再根据圆周角定理得到∠BDC=90°,则可判断DM为Rt△ADC斜边上的中线,所以DM=CM=4,根据等腰三角形的性质得∠1=∠2,加上∠3=∠4,则∠1+∠3=∠2+∠4=90°,即∠ODM=90°,然后根据切线得判定定理即可得到直线DM是圆O的切线;
(2)先证明Rt△EOD∽Rt△EMD,利用相似比可得到OE=
EC-3,再在Rt△EOC中利用勾股定理得到32+EC2=(
EC-3)2,解得EC=
,然后利用正切的定义求解.
(2)先证明Rt△EOD∽Rt△EMD,利用相似比可得到OE=
| 4 |
| 3 |
| 4 |
| 3 |
| 9 |
| 2 |
解答: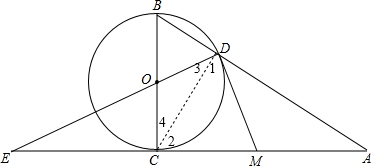 (1)证明:连结CD,如图,
(1)证明:连结CD,如图,
∵∠ACB=90°,BC=6,AB=10,
∴AC=
=8,
∵CM=4,
∴CM=AM=4,
∵BC为直径,
∴∠BDC=90°,
∴DM为Rt△ADC斜边上的中线,
∴DM=CM=4,
∴∠1=∠2,
∵OD=OC,
∴∠3=∠4,
∴∠1+∠3=∠2+∠4,即∠OCM=∠ODM,
而∠OCM=90°,
∴∠ODM=90°,
∴OD⊥DM,
∴直线DM是圆O的切线;
(2)解:∵∠OEC=∠MED,
∴Rt△EOD∽Rt△EMD,
∴
=
,即
=
,
∴OE=
EC-3,
在Rt△EOC中,∵OC2+EC2=OE2,
∴32+EC2=(
EC-3)2,
解得EC=
,
∴tanE=
=
=
.
 (1)证明:连结CD,如图,
(1)证明:连结CD,如图,∵∠ACB=90°,BC=6,AB=10,
∴AC=
| AB2-BC2 |
∵CM=4,
∴CM=AM=4,
∵BC为直径,
∴∠BDC=90°,
∴DM为Rt△ADC斜边上的中线,
∴DM=CM=4,
∴∠1=∠2,
∵OD=OC,
∴∠3=∠4,
∴∠1+∠3=∠2+∠4,即∠OCM=∠ODM,
而∠OCM=90°,
∴∠ODM=90°,
∴OD⊥DM,
∴直线DM是圆O的切线;
(2)解:∵∠OEC=∠MED,
∴Rt△EOD∽Rt△EMD,
∴
| EC |
| ED |
| OC |
| DM |
| EC |
| 3+OE |
| 3 |
| 4 |
∴OE=
| 4 |
| 3 |
在Rt△EOC中,∵OC2+EC2=OE2,
∴32+EC2=(
| 4 |
| 3 |
解得EC=
| 9 |
| 2 |
∴tanE=
| OC |
| EC |
| 3 | ||
|
| 2 |
| 3 |
点评:本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了勾股定理和相似三角形的判定与性质.

练习册系列答案
相关题目
若|a|+|b|=|a+b|成立,那么( )
| A、a,b同号 |
| B、a,b异号 |
| C、a,b的绝对值相等 |
| D、a,b同号或a,b中至少有一个为0 |
下列问题中,两个变量成正比例的是( )
| A、等腰三角形的面积一定,它的底边和底边上的高 |
| B、等边三角形的面积和它的边长 |
| C、长方形的一边长确定,它的周长与另一边长 |
| D、长方形的一边长确定,它的面积与另一边长 |