题目内容
19. 如图,在△ABC中,AD⊥BC于D,BD=AD,DG=DC,E,F分别是BG,AC的中点.
如图,在△ABC中,AD⊥BC于D,BD=AD,DG=DC,E,F分别是BG,AC的中点.(1)求证:DE=DF,DE⊥DF;
(2)连接EF,若AC=10,求EF的长.
分析 (1)证明△BDG≌△ADC,根据全等三角形的性质、直角三角形的性质证明;
(2)根据直角三角形的性质分别求出DE、DF,根据勾股定理计算即可.
解答 (1)证明:∵AD⊥BC,
∴∠ADB=∠ADC=90°,
在△BDG和△ADC中,
$\left\{\begin{array}{l}{BD=AD}\\{∠BDG=∠ADC}\\{DG=DC}\end{array}\right.$,
∴△BDG≌△ADC,
∴BG=AC,∠BGD=∠C,
∵∠ADB=∠ADC=90°,E,F分别是BG,AC的中点,
∴DE=$\frac{1}{2}$BG=EG,DF=$\frac{1}{2}$AC=AF,
∴DE=DF,∠EDG=∠EGD,∠FDA=∠FAD,
∴∠EDG+∠FDA=90°,
∴DE⊥DF;
(2)解:∵AC=10,
∴DE=DF=5,
由勾股定理得,EF=$\sqrt{D{E}^{2}+D{F}^{2}}$=5$\sqrt{2}$.
点评 本题考查的是全等三角形的判定和性质、直角三角形的性质以及勾股定理的应用,掌握全等三角形的判定定理和性质定理是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.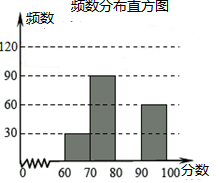 某校举行了”文明河南中小学生知识竞赛“活动,并随即抽查了部分同学的成绩,整理并制作成图表如下:
某校举行了”文明河南中小学生知识竞赛“活动,并随即抽查了部分同学的成绩,整理并制作成图表如下:
请根据以上图表提供的信息,解答下列问题:
(1)请求出:m=120,n=0.3,抽查的总人数为300人;
(2)请补全频数分布直方图;
(3)抽查成绩的中位数应落在80≤x<90分数段内;
(4)如果比赛成绩在80分以上(含80分)为优秀,任意抽取一位同学,则成绩优秀的概率为多少?
 某校举行了”文明河南中小学生知识竞赛“活动,并随即抽查了部分同学的成绩,整理并制作成图表如下:
某校举行了”文明河南中小学生知识竞赛“活动,并随即抽查了部分同学的成绩,整理并制作成图表如下:| 分数段 | 频数 | 频率 |
| 60≤x<70 | 30 | 0.1 |
| 70≤x<80 | 90 | n |
| 80≤x<90 | m | 0.4 |
| 90≤x≤100 | 60 | 0.2 |
(1)请求出:m=120,n=0.3,抽查的总人数为300人;
(2)请补全频数分布直方图;
(3)抽查成绩的中位数应落在80≤x<90分数段内;
(4)如果比赛成绩在80分以上(含80分)为优秀,任意抽取一位同学,则成绩优秀的概率为多少?
10.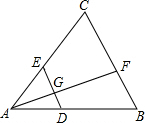 如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,点F为BC边上一点,连接AF交DE于点G,则下列结论中一定正确的是( )
如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,点F为BC边上一点,连接AF交DE于点G,则下列结论中一定正确的是( )
 如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,点F为BC边上一点,连接AF交DE于点G,则下列结论中一定正确的是( )
如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,点F为BC边上一点,连接AF交DE于点G,则下列结论中一定正确的是( )| A. | $\frac{AD}{AB}$=$\frac{AE}{EC}$ | B. | $\frac{AG}{GF}$=$\frac{AE}{BD}$ | C. | $\frac{BD}{AD}$=$\frac{CE}{AE}$ | D. | $\frac{AG}{AF}$=$\frac{AC}{EC}$ |
7.下列算式运算结果正确的是( )
| A. | (2x5)2=2x10 | B. | (-3)-2=$\frac{1}{9}$ | C. | (a+1)2=a2+1 | D. | a-(a-b)=-b |
4.下列运算正确的是( )
| A. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | B. | ${({-\frac{1}{2}x{y^2}})^3}=-\frac{1}{6}{x^3}{y^6}$ | ||
| C. | (-x)5÷(-x)2=x3 | D. | $\sqrt{18}+\root{3}{-64}=3\sqrt{2}-4$ |
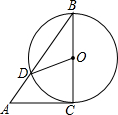 如图,AC是⊙O的切线,切点为C,BC是⊙O的直径,AB交⊙O于点D,连接OD,若∠A=50°,则∠COD的度数为80°.
如图,AC是⊙O的切线,切点为C,BC是⊙O的直径,AB交⊙O于点D,连接OD,若∠A=50°,则∠COD的度数为80°.