题目内容
14．
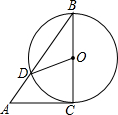如图，AC是⊙O的切线，切点为C，BC是⊙O的直径，AB交⊙O于点D，连接OD，若∠A=50°，则∠COD的度数为80°．
分析 根据切线的性质得出∠C=90°，再由已知得出∠ABC，由外角的性质得出∠COD的度数．
解答 解：∵AC是⊙O的切线，
∴∠C=90°，
∵∠A=50°，
∴∠B=40°，
∵OB=OD，
∴∠B=∠ODB=40°，
∴∠COD=2×40°=80°，
故答案为80°．
点评 本题考查了切线的性质，掌握切线的性质、直角三角形的性质以及外角的性质是解题的关键．
练习册系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
已知在平面直角坐标系xOy中（如图），已知抛物线y=-x2+bx+c经过点A（2，2），对称轴是直线x=1，顶点为B．
5．抛物线y=-$\frac{3}{5}$（x+$\frac{1}{2}$）2-3的顶点坐标是（ ）
| A． | （$\frac{1}{2}$，-3） | B． | （-$\frac{1}{2}$，-3） | C． | （$\frac{1}{2}$，3） | D． | （-$\frac{1}{2}$，3） |
9．若关于x的方程kx2-3x-$\frac{9}{4}$=0有实数根，则实数k的取值范围是（ ）
| A． | k=0 | B． | k≥-1且k≠0 | C． | k≥-1 | D． | k＞-1 |
如图，在△ABC中，AD⊥BC于D，BD=AD，DG=DC，E，F分别是BG，AC的中点．
6．有一个数值转换器，原理如下：当输入的x为64时，输出的y是（ ）
| A． | $2\sqrt{2}$ | B． | $3\sqrt{2}$ | C． | $2\sqrt{3}$ | D． | 8 |
3．已知a=-2，则代数式a+1的值为（ ）
| A． | -3 | B． | -2 | C． | -1 | D． | 1 |
4．
如图，△ABC的面积是12，点D、E、F、G分别是BC、AD、BE、CE的中点，则△AFG的面积是（ ）
如图，△ABC的面积是12，点D、E、F、G分别是BC、AD、BE、CE的中点，则△AFG的面积是（ ）| A． | 4.5 | B． | 5 | C． | 5.5 | D． | 6 |