题目内容
17.(1)计算:5$\sqrt{\frac{1}{5}}$+$\frac{1}{2}$$\sqrt{20}$-$\sqrt{\frac{5}{4}}$×$\sqrt{\frac{4}{5}}$+$\sqrt{45}$÷$\sqrt{5}$(2)计算:|-$\frac{1}{2}$|-$\sqrt{9}$+(π-4)0-2-1.
分析 (1)先进行二次根式的乘除运算,然后把各二次根式化简后合并即可;
(2)根据零指数幂与负整数整数幂的意义计算.
解答 解:(1)原式=$\sqrt{5}$+$\sqrt{5}$-1+$\sqrt{9}$
=2$\sqrt{5}$-1+3
=2$\sqrt{5}$+2;
(2)原式=$\frac{1}{2}$-3+1-$\frac{1}{2}$
=-2.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.也考查了零指数幂与负整数整数幂.

练习册系列答案
相关题目
12.下列方程为一元一次方程的是( )
| A. | y=0 | B. | 3x+2y=3 | C. | x2=2x | D. | $\frac{1}{y}+y=2$ |
9.根据下表中的对应值,判断一元二次方程x2-4x+2=0的一个解的取值范围是0.5<x<1.
| x | 0 | 0.5 | 1 | 1.5 |
| x2-4x+2 | 2 | 0.25 | -1 | -1.75 |
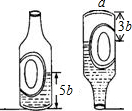 小聪量了自己喝的矿泉水瓶瓶底的直径为a厘米,瓶中水的高度为5b厘米,如图所示,他把矿泉水瓶颠倒过来测量了上面空瓶部分的高度为3b厘米(瓶子和瓶盖的厚度忽略不计),用a,b表示这个瓶子的容积为2πa2b立方厘米.
小聪量了自己喝的矿泉水瓶瓶底的直径为a厘米,瓶中水的高度为5b厘米,如图所示,他把矿泉水瓶颠倒过来测量了上面空瓶部分的高度为3b厘米(瓶子和瓶盖的厚度忽略不计),用a,b表示这个瓶子的容积为2πa2b立方厘米.