题目内容
3.根据完全平方公式填空:(1)x2+2xy+y2=(x+y)2
(2)($\frac{3x}{4}$)2+$\frac{3}{2}$xy+y2=($\frac{3x}{4}$+y)2.
分析 (1)根据完全平方公式得出即可;
(2)根据完全平方公式得出即可.
解答 解:(1)x2+2xy+y2=(x+y)2,
故答案为:y2,x+y;
(2)($\frac{3x}{4}$)2+$\frac{3}{2}$xy+y2=($\frac{3x}{4}$+y)2,
故答案为:$\frac{3x}{4}$,$\frac{3x}{4}$+y.
点评 本题考查了完全平方公式,能熟记公式的特点是解此题的关键,注意:(a+b)2=a2+2ab+b2,(a-b)2=a2-2ab+b2.

练习册系列答案
相关题目
14.11日凌晨,阿里巴巴公布了2015双十一购物狂欢节的相关数据:33分53秒时,成交额破200亿.200亿用科学记数法表示为( )
| A. | 0.2×1010 | B. | 2×1010 | C. | 2×109 | D. | 20×109 |
11.在-1、0、1、2这四个数中,最小的数是( )
| A. | -1 | B. | 0 | C. | 1 | D. | 1 |
15.小伟掷一枚质地均匀的骰子,骰子的六个面上分别刻有1到6的点数,下列事件是不可能事件的是( )
| A. | 掷一次骰子,在骰子向上的一面上的点数大于0 | |
| B. | 掷一次骰子,在骰子向上的一面上的点数为6 | |
| C. | 掷两次骰子,在骰子向上的一面上的点数之和刚好为12 | |
| D. | 掷两次骰子,在骰子向上的一面上的点数之和刚好为13 |
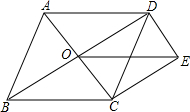 如图,在菱形ABCD中,对角线AC与BD相交于点O,CE∥BD,DE∥AC,连接OE.
如图,在菱形ABCD中,对角线AC与BD相交于点O,CE∥BD,DE∥AC,连接OE.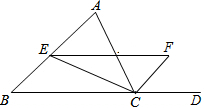 如图,在△ABC中,CE平分∠ACB,CF平分外角∠ACD,若CE=4cm,CF=3cm,则EF的长为5cm.
如图,在△ABC中,CE平分∠ACB,CF平分外角∠ACD,若CE=4cm,CF=3cm,则EF的长为5cm.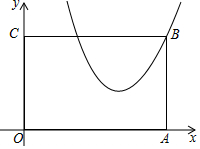 矩形OABC在平面直角坐标系内的位置如图所示,点O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,点B的坐标为(5,4).将矩形OABC沿某直线1对折,使点B落在坐标轴上的点F处,且BF与1的交点Q恰好落在过点B的抛物线y=x2+mx+14上,则点F的坐标为(1,0)或(3,0)或(0,$\frac{3}{2}$).
矩形OABC在平面直角坐标系内的位置如图所示,点O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,点B的坐标为(5,4).将矩形OABC沿某直线1对折,使点B落在坐标轴上的点F处,且BF与1的交点Q恰好落在过点B的抛物线y=x2+mx+14上,则点F的坐标为(1,0)或(3,0)或(0,$\frac{3}{2}$).