题目内容
18.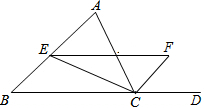 如图,在△ABC中,CE平分∠ACB,CF平分外角∠ACD,若CE=4cm,CF=3cm,则EF的长为5cm.
如图,在△ABC中,CE平分∠ACB,CF平分外角∠ACD,若CE=4cm,CF=3cm,则EF的长为5cm.
分析 根据角平分线的定义可以证明出△CEF是直角三角形,由勾股定理求出EF即可.
解答  解:如图所示:
解:如图所示:
∵CE平分∠ACB交AB于E,CF平分∠ACD,
∴∠1=∠2=$\frac{1}{2}$∠ACB,∠3=∠4=$\frac{1}{2}$∠ACD,
∴∠2+∠3=$\frac{1}{2}$(∠ACB+∠ACD)=90°,
∴△CEF是直角三角形,
∴EF=$\sqrt{C{E}^{2}+C{F}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5(cm);
故答案为:5.
点评 本题考查的是勾股定理以及角平分线的定义,证明出△CEF是直角三角形是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.小红利用一些花布的边角料,剪裁后装饰手工画,下面四个图案是她剪裁出的空心等边三角形、菱形、矩形、正方形,若每个图案花边的宽度都相等,那么每个图案中花边的内外边缘所围成的几何图形不一定相似的是( )
| A. |  | B. |  | C. |  | D. |  |
9.计算(-2)100+(-2)101所得的结果是( )
| A. | 2100 | B. | -1 | C. | -2 | D. | -2100 |
6.已知a1=$\frac{x}{x+2}$,a2=$\frac{{a}_{1}}{{a}_{1}+2}$,…an=$\frac{{a}_{n-1}}{{a}_{n-1}+2}$,其中n是正整数,则a8的值为( )
| A. | $\frac{x}{15x+16}$ | B. | $\frac{x}{127x+128}$ | C. | $\frac{x}{255x+256}$ | D. | $\frac{x}{511x+512}$ |
13. 一个几何体的三视图如图所示,则这个几何体是( )
一个几何体的三视图如图所示,则这个几何体是( )
 一个几何体的三视图如图所示,则这个几何体是( )
一个几何体的三视图如图所示,则这个几何体是( )| A. |  | B. |  | C. |  | D. |  |
10.下列各式中,计算错误的是( )
| A. | [(a+b)2]5=(a+b)10 | B. | [(a+b)2]n=(a+b)n+2 | C. | [(a+b)x]5=(a+b)5x | D. | [(a+b)m]n=(a+b)mn |
7.九年级学生从学校出发,去相距10km的博物馆参观,第一组学生骑自行车先走,过了20分钟后,第二组学生乘汽车出发,结果两组学生同时到达,第二组学生的速度是第一组学生速度的2倍,设第一组学生的速度为xkm/h,则所列方程正确的是( )
| A. | $\frac{10}{x}$-$\frac{10}{2x}$=20 | B. | $\frac{10}{2x}$-$\frac{10}{x}$=20 | C. | $\frac{10}{2x}$-$\frac{10}{x}$=$\frac{1}{3}$ | D. | $\frac{10}{x}$-$\frac{10}{2x}$=$\frac{1}{3}$ |
3.若a+b=2,则代数式a2-b2+4b的值是( )
| A. | 2 | B. | 4 | C. | -2 | D. | -4 |