题目内容
19.已知x<0,x-x-1=-1,则x3+x-3的值是-2$\sqrt{5}$.分析 利用完全平方公式的性质,将x-x-1=-1,变形(x-x-1)2=(-1)2,得出x2+x-2的值,进而得出(x+x-1)的值,然后利用立方差公式进行变形,得出它的值.
解答 解:∵x-x-1=-1,(x-x-1)2=(-1)2,
∴x2+x-2-2=1,xx-1=1,
∴x2+x-2=3,
∵(x+x-1)2=x2+x-2+2xx-1=3+2=5,
∴x+x-1=±$\sqrt{5}$,
∵x<0,∴x+x-1=-$\sqrt{5}$,
∵x3+x-3=(x+x-1)(x2+x-2-xx-1),
=-$\sqrt{5}$×(3-1),
=-2$\sqrt{5}$,
故答案为:-2$\sqrt{5}$.
点评 此题主要考查了完全平方公式与立方和公式的应用,解决问题的关键是灵活分解因式,进行求解.

练习册系列答案
相关题目
10.3-2与32的关系为( )
| A. | 互为相反数 | B. | 互为倒数 | C. | 和为零 | D. | 绝对值相等 |
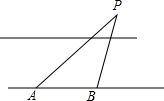 在沿东西走向的河岸南岸,某人自西向东行走,在A处测得河北岸建筑物P在北偏东60°的方向上,某人由A向东走400米到达B处时,在B处测得河北岸物P在北偏东45°的方向上,如果建筑物P距河北岸100米,求河宽.(人与河的距离忽略不计,$\sqrt{3}$≈1.7)
在沿东西走向的河岸南岸,某人自西向东行走,在A处测得河北岸建筑物P在北偏东60°的方向上,某人由A向东走400米到达B处时,在B处测得河北岸物P在北偏东45°的方向上,如果建筑物P距河北岸100米,求河宽.(人与河的距离忽略不计,$\sqrt{3}$≈1.7)