题目内容
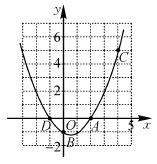
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0;②2a+b=0;③当m≠1时,a+b>a m2+bm;④a-b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=2.其中正确的有( )
m2+bm;④a-b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=2.其中正确的有( )
A.①②③ B.②④ C.②⑤ D.②③⑤

D
解析:∵图象开口向下,∴a<0.∵对称轴x=- =1,∴b=-2a,得b>0,2a+b=0.∵坐标轴与抛物线交点在y轴正半轴,∴c>0,∴abc<0,故①错,②对;排除A;∵对称轴是x=1,∴y最大值为a+b+c,当x=m(m≠1)时,y=am2+bm+c,可知a+b+c>am2+bm+c,故当m≠1时,a+b>am2+bm,故③对,可得答案D.
=1,∴b=-2a,得b>0,2a+b=0.∵坐标轴与抛物线交点在y轴正半轴,∴c>0,∴abc<0,故①错,②对;排除A;∵对称轴是x=1,∴y最大值为a+b+c,当x=m(m≠1)时,y=am2+bm+c,可知a+b+c>am2+bm+c,故当m≠1时,a+b>am2+bm,故③对,可得答案D.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (k≠0)的图象都经过点A(a,2).
(k≠0)的图象都经过点A(a,2).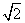 ,
,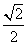 )是否在该反比例函数的图象上,请说明理由.
)是否在该反比例函数的图象上,请说明理由.