题目内容
如图，已知二次函数y=ax2+bx+c的图象过A(2,0)，B(0，-1)和C(4,5)三点.
(1)求二次函数的解析式；
(2)设二次函数的图象与x轴的另一个交点为D，求点D的坐标；
(3)在同一坐标系中画出直线y=x+1,并写出当x在什么范围内时，一次函数的值大于二次函数的值？
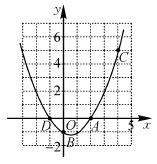
(1)∵二次函数的图象过B(0，-1)，
∴二次函数解析式为y=ax2+bx-1.
∵二次函数的图象过A(2,0)和C(4,5)两点，
∴
解得
∴y=
x2-x-1.
(2)当y=0时，x2-x-1=0，
解得x=2或x=-1，
∴D(-1,0).
(3)如图，当-1＜x＜4时一次函数的值大于二次函数的值.
练习册系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
x的图象向上平移2个单位，平移后，若y＞0，则x的取值范围是( )
的图象经过点(2,3)，那么下列四个点中，也在这个函数图象上的是( )
(x>0)的图象上有点P1，P2，P3，…，Pn，Pn+1，点P1的横坐标为2，且后面每个点的横坐标与它前面相邻点的横坐标的差都是2，过点P1，P2，P3，…，Pn，Pn+1分别作x轴，y轴的垂线段，构成若干个矩形，如图所示，将图中阴影部分的面积从左至右依次记为S1，S2，S3，…，Sn，则S1= ，Sn= .(用含n的代数式表示)
m2+bm；④a-b+c＞0；⑤若ax12+bx1＝ax22+bx2，且x1≠x2，则x1+x2＝2.其中正确的有( )
D.y=x2-1九(1)班数学兴趣小组经过市场调查，整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如下表：
| 时间x(天) | 1≤x＜50 | 50≤x≤90 |
| 售价(元/件) | x+40 | 90 |
| 每天销量(件) | 200-2x |
已知该商品的进价为每件30元，设销售该商品的每天利润为y元.
(1)求y与x的函数关系式；
(2)问销售该商品第几天时，每天销售利润最大，最大利润是多少？
(3)该商品在销售过程中，共有多少天每天销售利润不低于4 800元？请直接写出结果.