题目内容
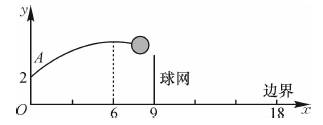
如图，排球运动员站在点O处练习发球，将球从O点正上方2 m的A处发出，把球看成点，其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x-6)2+h.已知球网与O点的水平距离为9 m，高度为2.43 m，球场的边界距O点的水平距离为18 m.
(1)当h=2.6时，求y与x的关系式(不要求写出自变量x的取值范围)；
(2)当h=2.6时，球能否越过球网？球会不会出界？请说明理由；
(3)若球一定能越过球网，又不出边界，求h的取值范围.
∵点(0，2)在y=a(x-6)2+h的图象上，
∴2=a
(0-6)2+h，a=
，
函数可写成y=(x-6)2+h.
(1)当h=2.6时，y与x的关系式是
y=-
(x-6)2+2.6；
(2)球能越过球网，球会出界.
理由：当x=9时，y=-×(9-6)2+2.6=2.45＞2.43，所以球能过球网；
当y=0时，-(x-6)2+2.6=0，解得x1=6+2
＞18，x2=6-2(舍去)，故球会出界.
另解：当x=18时，y=-×(18-6)2+2.6=0.2＞0，所以球会出界.
(3)由球能越过球网可知，当x=9时，y=
+h＞2.43，①
由球不出边界可知，当x=18时，y=8-3h≤0，②
由①、②知h≥
，所以h的取值范围是h≥.
练习册系列答案
相关题目
的图象经过点A(-2，3)，则当x＝-3时，y＝ .
m2+bm；④a-b+c＞0；⑤若ax12+bx1＝ax22+bx2，且x1≠x2，则x1+x2＝2.其中正确的有( )