题目内容
4.小亮解方程组$\left\{\begin{array}{l}{2x+y=●}\\{2x-y=12}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=5}\\{y=★}\end{array}\right.$,由于不小心滴上了两滴墨水,刚好遮住了两个数●和★,则两个数●与★的值为( )| A. | $\left\{\begin{array}{l}{●=8}\\{★=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{●=-8}\\{★=-2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{●=-8}\\{★=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{●=8}\\{★=-2}\end{array}\right.$ |
分析 根据题意可以分别求出●与★的值,本题得以解决.
解答 解:∵方程组$\left\{\begin{array}{l}{2x+y=●}\\{2x-y=12}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=5}\\{y=★}\end{array}\right.$,
∴将x=5代入2x-y=12,得y=-2,
将x=5,y=-2代入2x+y得,2x+y=2×5+(-2)=8,
∴●=8,★=-2,
故选D.
点评 本题考查二元一次方程组的解,解题的关键是明确题意,求出所求数的值.

练习册系列答案
相关题目
14.一次函数y=kx+b(k≠0)的图象与x轴,y轴分别交于A(-3,0),B(0,2),当函数图象在第二象限时,自变量x的取值范围是( )
| A. | -3<x<0 | B. | x<0 | C. | -3<x<2 | D. | x>-3 |
19. 双曲线y1,y2在第一象限的图象如图所示,其中y1的解析式为y1=$\frac{4}{x}$,过y1图象上的任意一点A,作x轴的平行线交y2图象于B,交y轴于C,若S△AOB=1,则y2的解析式是 ( )
双曲线y1,y2在第一象限的图象如图所示,其中y1的解析式为y1=$\frac{4}{x}$,过y1图象上的任意一点A,作x轴的平行线交y2图象于B,交y轴于C,若S△AOB=1,则y2的解析式是 ( )
 双曲线y1,y2在第一象限的图象如图所示,其中y1的解析式为y1=$\frac{4}{x}$,过y1图象上的任意一点A,作x轴的平行线交y2图象于B,交y轴于C,若S△AOB=1,则y2的解析式是 ( )
双曲线y1,y2在第一象限的图象如图所示,其中y1的解析式为y1=$\frac{4}{x}$,过y1图象上的任意一点A,作x轴的平行线交y2图象于B,交y轴于C,若S△AOB=1,则y2的解析式是 ( )| A. | y2=$\frac{3}{x}$ | B. | y2=$\frac{5}{x}$ | C. | y2=$\frac{6}{x}$ | D. | y2=$\frac{7}{x}$ |
16.已知三角形三边长为5、7、x,则x的取值范围是( )
| A. | x>2 | B. | x<12 | C. | 2<x<12 | D. | x>7 |
 如图,一个圆环面绕着过圆心的直线l旋转180°,想象并说出它形成的几何体的结构特征.
如图,一个圆环面绕着过圆心的直线l旋转180°,想象并说出它形成的几何体的结构特征.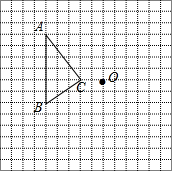 在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).画出绕点O逆时针旋转 90° 后的△A′B′C′.
在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).画出绕点O逆时针旋转 90° 后的△A′B′C′. 如图,正方形ABCD的顶点C,D在反比例函数y=$\frac{8}{x}$(x>0)的图象上,顶点A,B分别在x轴和y轴的正半轴上,再在其右侧作正方形EFDG,顶点G在反比例函数y=$\frac{8}{x}$(x>0)的图象上,顶点E在x轴的正半轴上,则点G的坐标为(2$\sqrt{3}$+2,2$\sqrt{3}$-2).
如图,正方形ABCD的顶点C,D在反比例函数y=$\frac{8}{x}$(x>0)的图象上,顶点A,B分别在x轴和y轴的正半轴上,再在其右侧作正方形EFDG,顶点G在反比例函数y=$\frac{8}{x}$(x>0)的图象上,顶点E在x轴的正半轴上,则点G的坐标为(2$\sqrt{3}$+2,2$\sqrt{3}$-2). 如图,在平面直角坐标系xOy中,点A的坐标为(-3,0)等边△AOC经过平移或轴对称或旋转都可以得到△OBD.
如图,在平面直角坐标系xOy中,点A的坐标为(-3,0)等边△AOC经过平移或轴对称或旋转都可以得到△OBD. 如图,将三角形ABE沿着BC的方向平移到三角形FCD的位置,若AB=4cm,AE=3cm,BE=3cm,BC=5cm,则CF,CD,DF,EF的长分别是多少?
如图,将三角形ABE沿着BC的方向平移到三角形FCD的位置,若AB=4cm,AE=3cm,BE=3cm,BC=5cm,则CF,CD,DF,EF的长分别是多少?